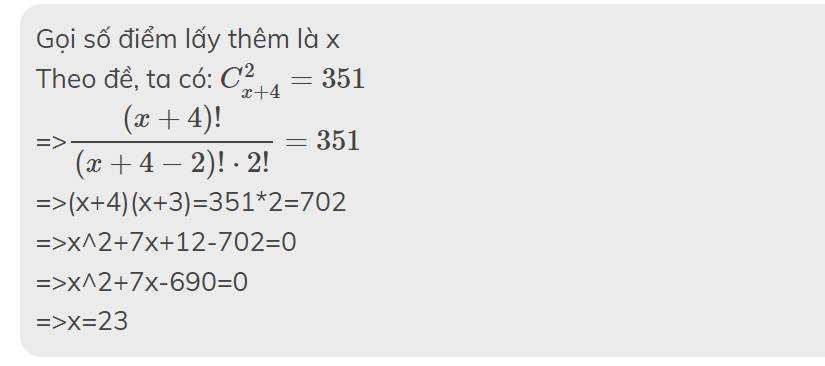Cho M là trung điểm của đoạn thẳng AB. Trên đường trung trực của AB lấy 3 điểm phân biệt D; E; F(khác điểm M). Nối các điểm D; E; F với A, B. Trên hình vẽ có mấy cặp tam giác bằng nhau ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a ) Vì C là trung điểm của AB
=> BC = AB / 2 = 6 / 2 = 3 cm
Vì D là trung điểm của BC
=> CD = BC / 2 = 3 / 2 = 1,5 cm
Vì AC và AD là 2 tia đối nhau
nên C nằm giữa A và D
=> AC + CD = AD
=> AD = 3 +1,5 = 4,5 cm
Vậy AD = 4,5 cm
Nếu bạn thấy chỗ nào chx hiểu để mình làm lại cho dễ hiểu hơn

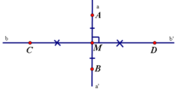
Ta có: b b ' ⊥ a a ' nên b b ' ⊥ A B tại (vì hai điểm và thuộc đường thẳng aa' ) (1)
và M là trung điểm của AB (2)
Từ (1) và (2) suy ra nên bb' là đường trung trực của AB (theo định nghĩa đường trung trực)
Tương tự: aa' là đường trung trực của CD.

Chọn A.
Gọi I là tâm mặt cầu đi qua hai điểm A, B cố định và phân biệt thì ta luôn có IA = IB. Do đó I thuộc mặt phẳng trung trực của đoạn AB.

Bài 2:
a: Vì OA<OB
nên A nằm giữa O và B
=>OA+AB=OB
=>AB=4cm
b: Vì AO và AM là hai tia đối nhau
nen A nằm giữa O và M
c: AM=AB/2=2cm

Gọi số điểm lấy thêm là x
Theo đề, ta có: \(C^2_{x+4}=351\)
=>\(\dfrac{\left(x+4\right)!}{\left(x+4-2\right)!\cdot2!}=351\)
=>(x+4)(x+3)=351*2=702
=>x^2+7x+12-702=0
=>x^2+7x-690=0
=>x=23