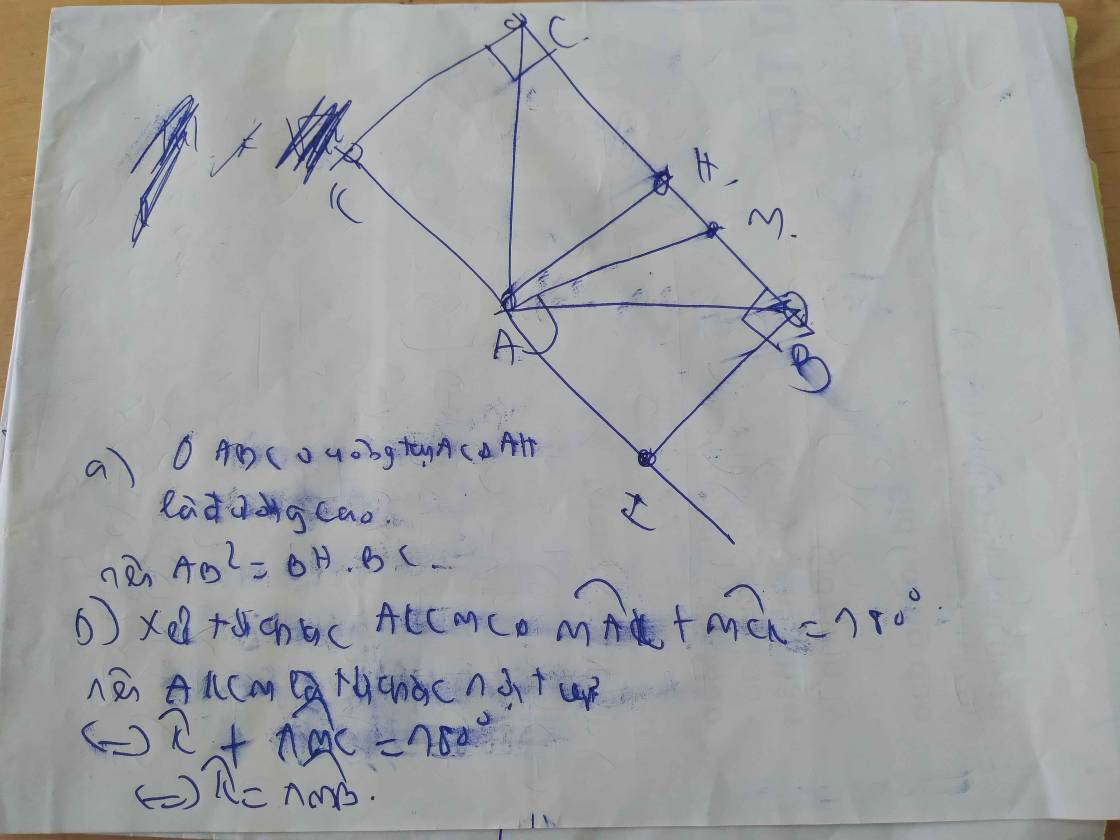
Cho tam giác ABC vuông cân tại A. Trên cubgf một nửa mặt phẳng chứa A bờ BC vẽ các tia Bx,Cy cùng vuông góc với BC. Lấy M nằm giữa B và C. Đường thẳng vuông góc với AM tại A cắt Bx và Cy lần lượt tại H và K. Chứng minh
a) BM = CK
b) A là trung điểm của HK
c) Gọi P là giao điểm của AB và MH và Q là giao của AC và MK. Chứng minh PQ//BC