Cho hình chóp SABCD có ABCD là hình bình hàng tâm O. Gọi M,N,P lần lượt là các điểm thuộc đoạn AB, AC, SO ( M không trùng với A và B, N không trùng với B và C, P không trùng với S và O).
a. Tìm giao điểm của (MNP) với các đoạn thẳng chứa các cạnh của hình chóp đã cho.
b. Suy ra thiết diện tạo bởi ( MNP) và hình chóp SABCD.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
4 tháng 3 2019
Chọn B.
Phương pháp:
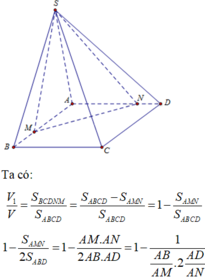
Tỉ lệ thể tích của các khối chóp .S ABCD và .S MBCDN bằng tỉ lệ diện tích các đa giác ABCD và MBCDN .
Cách giải:
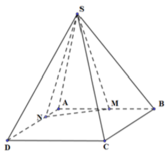
Do các khối chóp .S ABCD và S.MBCDN có cùng chiều cao kẻ từ S nên
CM
26 tháng 12 2018
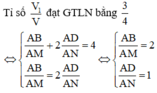
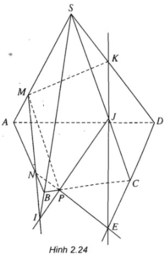
a lần lượt tìm giao điểm của mặt phẳng (MNP) với các đường thẳng chứa các cạnh của hình chóp.
Gọi I = MN ∩ SB
Ta có:
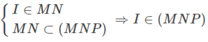
Vậy I = SB ∩ (MNP).
Từ đó, làm tương tự ta tìm được giao điểm của (MNP) với các cạnh còn lại.
Cụ thể :
Gọi J = IP ∩ SC, ta có J = SC ∩ (MNP)
Gọi E = NP ∩ CD, ta có E = CD ∩ (MNP)
Gọi K = JE ∩ SD, ta có K = SD ∩ (MNP)
CM
9 tháng 4 2019
Chọn đáp án A
Đặt A B A M = x và A D A N = y x , y ≥ 1
Từ giả thiết ta có x + 2 y = 4 1
Suy ra
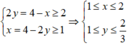
Ta có
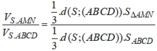
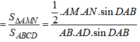
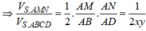
Từ (1) và (2) suy ra V 1 V = 1 - 1 x 4 - x
Áp dụng bất đẳng thức cho hai số dương x và 4 – x ta có:
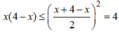
Dấu “=” xảy ra khi và chỉ khi
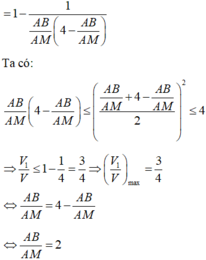
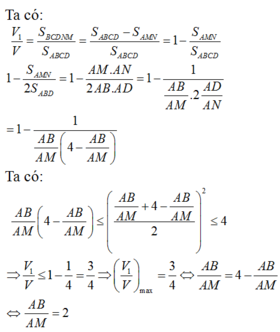
Bạn kham khảo tại link:
Cho hình chóp S.ABCD có đáy là hình bình hành tâm O. Gọi M, N, E là ba điểm lần lượt lấy trên AD, CD, SO. Tìm thiết diện của hình chóp bởi ( MNP) - Hình học không gian - Diễn đàn Toán học
Copy và dán:
https://diendantoanhoc.net/topic/125716-cho-h%C3%ACnh-ch%C3%B3p-sabcd-c%C3%B3-%C4%91%C3%A1y-l%C3%A0-h%C3%ACnh-b%C3%ACnh-h%C3%A0nh-t%C3%A2m-o-g%E1%BB%8Di-m-n-e-l%C3%A0-ba-%C4%91i%E1%BB%83m-l%E1%BA%A7n-l%C6%B0%E1%BB%A3t-l%E1%BA%A5y-tr%C3%AAn-ad-cd-so-t%C3%ACm-thi%E1%BA%BFt-di%E1%BB%87/
Học tốt!
thanks