Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B.
Phương pháp:
Tỉ lệ thể tích của các khối chóp .S ABCD và .S MBCDN bằng tỉ lệ diện tích các đa giác ABCD và MBCDN .
Cách giải:
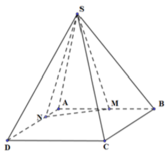
Do các khối chóp .S ABCD và S.MBCDN có cùng chiều cao kẻ từ S nên

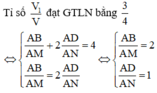

Đáp án C
Giả sử S D → = m . S M → ; S B → = n . S N → .
S A → + S C → = S B → + S D →
Do A; M; N; K đồng phẳng nên m + n = 3 .
V S . A K M V S . A B C = 1 2 .1. 1 m = 1 2 m ⇒ V S . A K M V = 1 4 m
Tương tự ta có V S . A K N V = 1 4 n ⇒ V ' V = 1 4 . m + n m n = 3 4 m n ≥ 3 m + n 2 = 3 3 2 = 1 3 .
Dấu bằng xảy ra khi m = n = 1,5 .

Đáp án C.

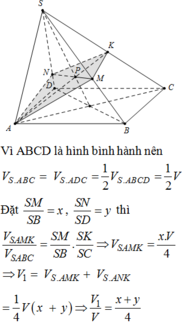
V 1 V = 1 2 V S . A M P V S . A D C + V S . A N P V S . A B C = 1 2 . S P S C S M S D + S N S B = x + y 4 V 1 V = 1 2 V S . A M N V S . A B D + V S . P M N V S . C B D = 1 2 . S M S D + S N S B 1 + S P S C = 3 x y 4 ⇒ x + y = 3 x y ⇒ y = x 3 x − 1 ∈ 0 ; 1 ⇒ x ∈ 1 2 ; 1 ⇒ V 1 V = 3 x 3 4 3 x − 1 = 3 4 f x .
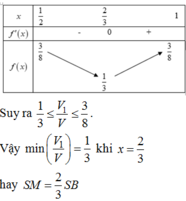
Xét f x = x 2 3 x − 1 với x ∈ 1 2 ; 1
Xét hàm, suy ra M a x 1 2 ; 1 f x = 1 2 ⇒ V 1 V ≤ 3 8 .

Đáp án C
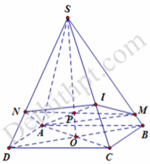
Bài toán sử dụng bổ đề sau: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Mặt phẳng (P) bất kì cắt các cạnh SA, SB, SC, SD lần lượt tại các điểm A’, B’, C’, D’ với tỉ số
S A ' S A = x ; S B ' S B = y ; S C ' S C = z ; S D ' S D = t thì ta có đẳng thức
1 x + 1 z = 1 y + 1 t và tỉ số
V S . A ' B ' C ' D ' V S . A B C D = x y z t 4 1 x + 1 y + 1 z + 1 t
Áp dụng vào bài toán
đặt u = S M S B , v = S N S D ta có
1 u + 1 v = S A S A ' + S C S I = 1 1 + 1 2 3 = 5 2 ≥ 2 u v ≥ 16 25 ⇒ V ' V = u v .1. 2 3 4 1 u + 1 v + 1 1 + 1 2 3 = 5 u v 6 ≥ 8 15

Đáp án A

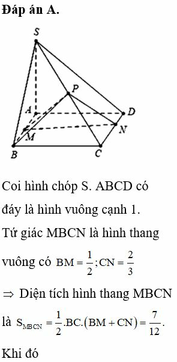
Coi hình chóp S.ABCD có đáy là hình vuông cạnh 1
Tứ giác MBCN là hình thang vuông có B M = 1 2 , C N = 2 3
⇒ Diện tích hình thang MBCN là S M B C N = 1 2 B C B M + C N = 7 12
Khi đó:
V P . M B C N = 1 3 d P ; A B C D . S M B C N = 1 3 . 1 2 d S ; A B C D . 7 12 S A B C D = 7 24 . 1 3 d S ; A B C D . S A B C D = 7 24 V S . A B C D = 7 24 .48 = 14

Đáp án C
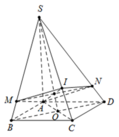
Gọi O là tâm của hình bình hành ABCD
Gọi H = S K ∩ A I qua H kẻ d / / B D cắt SB;SD lần lượt tại M;N
Xét tam giác SAC có
I S I C . A C O C . O H S H = 1 ⇒ O H S C = 1 4 ⇒ S H S C = 4 5
Mà M N / / B D → S M S B = S N S D = S H S O = 4 5
Ta có V S . A M I V S . A C D = S M S B . S I S C = 2 3 . S M S B ⇒ V S . A M I V S . A B C D = 1 3 . S M S B
Và V S . A N I V S . A C D = S N S D . S I S C = 2 3 . S D S D ⇒ V S . A N I V S . A B C D = 1 3 . S N S D
Suy ra V ' V = 1 3 S M S B + S N S D = 1 3 . 4 5 + 4 5 = 8 15
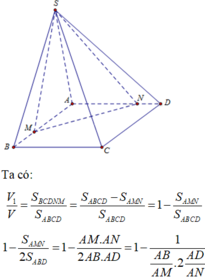
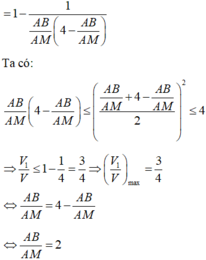
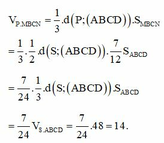
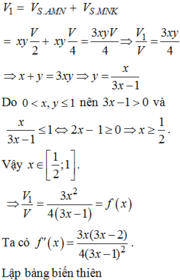
Chọn đáp án A
Đặt A B A M = x và A D A N = y x , y ≥ 1
Từ giả thiết ta có x + 2 y = 4 1
Suy ra
Ta có
Từ (1) và (2) suy ra V 1 V = 1 - 1 x 4 - x
Áp dụng bất đẳng thức cho hai số dương x và 4 – x ta có:
Dấu “=” xảy ra khi và chỉ khi