Cho hình vuông ABCD. Tính cos MAN biết rằng M, N theo thứ tự là trug điểm của BC, CD.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a,
Xét ABD, ta có :
MA = MB (gt)
QA = QD (gt)
=> MQ là đường trung bình.
=> MQ // BD và MQ = BD : 2 (1)
Cmtt, ta được :
NP // BD và NP = BD : 2 (2)
NM // AC và NM = AC : 2 (3)
Từ (1) và (2) : MQ // NP và MQ = PP
=> Tứ giác MNPQ làhình bình hành.
ta có :
AC = BD ( hai đường chéo hình thang cân ABCD)
NM = AC : 2 (cmt)
MQ = BD : 2 (cmt)
=> NM = MQ
Xét hình bình hành MNPQ, ta có :
NM = MQ (cmt)
=> hình bình hành MNPQ là hình thoi.
b , Nếu AC BD
NM // AC (cmt)
NP // BD (cmt)
=> NM NP tại N
Hay
Xét hình thoi MNPQ , ta có : (cmt)
=> hình thoi MNPQ là hình vuông.
tick nha bn

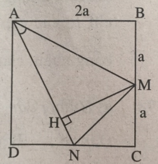
Kẻ đường cao MH của tam giác cân AMN. Ta có sin ∠ (NAM) = HM/AM và diện tích tam giác AMN là S A M N = 1/2AN.MH = 1/2AN.AM.sin(NAM) = 1/2 A N 2 .sin(NAM) = 1/2( A D 2 + D N 2 ). sin(NAM) = ( 5 a 2 )/2 sin(NAM).
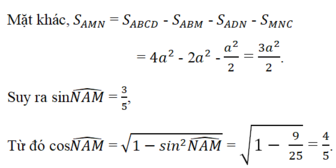

Vì \(\tan MAB=\frac{MB}{AB}=\frac{1}{2}\Rightarrow\widehat{MAB}=26,5°\)Tương tự có \(\widehat{NAD}=26,5°\)
\(\Rightarrow\widehat{MAN}=37°\Rightarrow\cos MAN=\cos37\approx0,79\)

Đặt AB=BC=CD=AD=2a
=>NC=MC=BM=DN=a
\(NM=\sqrt{a^2+a^2}=a\sqrt{2}\)
\(AM=\sqrt{\left(2a\right)^2+a^2}=a\sqrt{5}\)
\(AN=\sqrt{\left(2a\right)^2+a^2}=a\sqrt{5}\)
Xét ΔMAN có \(cosMAN=\dfrac{AM^2+AN^2-MN^2}{2\cdot AM\cdot AN}=\dfrac{5a^2+5a^2-2a^2}{2\cdot a\sqrt{5}\cdot a\sqrt{5}}\)
\(=\dfrac{8a^2}{10a^2}=\dfrac{4}{5}\)