2.Luyện tập ( SGK/ 97/hình học- chương 2)
Cho hình 32, trong mỗi trường hợp hình vẽ có hai đường thẳng song song với nhau. Tìm ra và kể tên 2 đường thẳng song song với nhau đó ? Giải thích cách hiểu của em.
Giúp mik nhanh nha ! Thanks trước !^3^
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
g mỗi trường hợp hình vẽ có hai đường thẳng song song với nhau. Tìm ra và kể tên hai đường thẳng song song với nhau đó. Giải thích các hiểu của em.
11 tháng 9 2017
bấm vào đây Câu hỏi của quynh nhu nguyen - Toán lớp 7 | Học trực tuyến
18 tháng 10 2017
Hình a
Ta có góc C+góc B=1100+700=1800
mà góc C và góc B là hai tróng trong cùng phía nên AB song song với DC
Hình b
Ta có góc DEF=góc HFE=1240 mà hai góc này ở vị trí so le trong nên DE song song với FH
Hình c
Ta có góc IKJ= góc LJK=900 mà hai góc này ở vị trí so le trong nên IK song song với JL
thôi còn lại bạn tự giải nhé mình mệt quá
18 tháng 10 2017
Top of Form
Hình a
Ta có góc C+góc B=1100+700=1800
mà góc C và góc B là hai tróng trong cùng phía nên AB song song với DC
Hình b
Ta có góc DEF=góc HFE=1240 mà hai góc này ở vị trí so le trong nên DE song song với FH
Hình c
Ta có góc IKJ= góc LJK=900 mà hai góc này ở vị trí so le trong nên IK song song với JL
thôi còn lại bạn tự giải nhé mình mệt quá
28 tháng 9 2021
\(a,\)So le trong: \(E_1 và F_2;E_2 và F_1\)
Đồng vị: \(E_1 và F_4;E_2 và F_3;E_3 và F_2;E_4 và F_1\)
Trong cùng phía: \(E_1 và F_1;E_2 và F_2\)
\(b,\widehat{F_1}=\widehat{F_3}=120^0\left(đối.đỉnh\right)\\ \widehat{F_2}+\widehat{F_3}=180^0\left(kề.bù\right)\Rightarrow\widehat{F_2}=180^0-120^0=60^0\\ \widehat{F_2}=\widehat{F_4}-60^0\left(đối.đỉnh\right)\)
\(c,C_1:\widehat{F_2}=\widehat{E_3}\left(=60^0\right)\)
Mà 2 góc này ở vị trí đồng vị nên \(a//b\)
\(C_2:\)\(\widehat{E_1}=\widehat{E_3}=60^0\left(đối.đỉnh\right)\Rightarrow\widehat{E_1}=\widehat{F_2}\left(=60^0\right)\)
Mà 2 góc này ở vị trí so le trong nên \(a//b\)
HP
28 tháng 9 2021
a. Các cặp góc:
- So le trong là: \(\widehat{E_1}\) và \(\widehat{F_2};\widehat{E_2}\) và \(\widehat{F_1}\)
- Đồng vị là: \(\widehat{E_4},\widehat{F_1};\widehat{E_3},\widehat{F_2};\widehat{E_2},\widehat{F_3};\widehat{E_1},\widehat{F_4}\)
- Trong cùng phía là: \(\widehat{E_1},\widehat{F_1};\widehat{E_2},\widehat{F_2}\)
b. Ta có: \(\widehat{F_1}=\widehat{F_3}=120^o\) (đối đỉnh)
\(\widehat{F_2}=180^o-\widehat{F_1}=180^o-120^o=60^o\)
\(\widehat{F_3}=120^o\)
\(\widehat{F_4}=\widehat{F_2}=60^o\) (đối đỉnh)
c.
C1: Ta có: \(\widehat{E_1}=\widehat{E_3}=60^o\) (đối đỉnh)
Ta thấy: \(\widehat{E_1}=\widehat{F_2}=60^o\)
=> a//b (so le trong)
C2: Ta có: \(\widehat{E_2}=180^o-\widehat{E_3}=180^o-60^o=120^o\)
Ta thấy: \(\widehat{E_2}=\widehat{F_1}=120^o\)
=> a//b (so le trong)
CM
6 tháng 12 2017
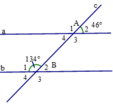
a) Ta có A ^ 2 + A ^ 3 = 180 ∘ mà A ^ 2 = 46 ∘
Do đó A ^ 3 = 180 ∘ − 46 ∘ = 134 ∘
Mặt khác B ^ 1 = 134 ∘
⇒ A ^ 3 = B ^ 1 mà hai góc này ở vị trí so le trong
=> a // b
b.
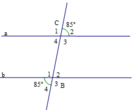
Ta có C ^ 2 = C ^ 4 = 85 ∘ (hai góc đối đỉnh)
mặt khác B ^ 4 = 85 ∘
⇒ A ^ 4 = B ^ 4 mà hai góc này ở vị trí so le trong
=> a // b
c.
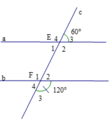
Ta có E ^ 2 + E ^ 3 = 180 ∘ (hai góc kề bù) mà E ^ 3 = 60 ∘
Do đó E ^ 2 = 180 ∘ − 60 ∘ = 120 ∘
Mặt khác F ^ 3 = 120 ∘
⇒ F ^ 3 = E ^ 2 mà hai góc này ở vị trí đồng vị
=> a // b
d.
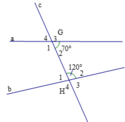
Ta có G ^ 1 + G ^ 2 = 180 ∘ (hai góc kề bù) mà G ^ 2 = 70 ∘
Do đó G ^ 1 = 180 ∘ − 70 ∘ = 110 ∘
Mà H ^ 2 = 120 ∘
⇒ G ^ 1 < H ^ 2 110 ∘ < 120 ∘ mà hai góc này ở vị trí so le trong
=> hai đường thẳng a và b không song song với nhau
HQ
Hà Quang Minh
Giáo viên
18 tháng 9 2023
1. Vì \(\widehat {BAx} = \widehat {CDA}( = 60^\circ )\)
Mà 2 góc này ở vị trí đồng vị
\( \Rightarrow \) AB//CD (Dấu hiệu nhận biết hai đường thẳng song song)
2. Ta có: \(\widehat {zKy'} + \widehat {y'Kz'} = 180^\circ \) ( 2 góc kề bù)
\(\begin{array}{l} \Rightarrow 90^\circ + \widehat {y'Kz'} = 180^\circ \\ \Rightarrow \widehat {y'Kz'} = 180^\circ - 90^\circ = 90^\circ \end{array}\)
Vì \(\widehat {yHz'} = \widehat {y'Kz'}\)
Mà 2 góc này ở vị trí đồng vị
\( \Rightarrow \) xy // x’y’ (Dấu hiệu nhận biết hai đường thẳng song song)
Chú ý:
2 đường thẳng cùng vuông góc với 1 đường thẳng thứ ba thì 2 đường thẳng đó song song.