Dựng hình tan giác ABC sao cho BC = a , đường cao AH = h , đường trung tuyến BM = k
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
24 tháng 4 2023
b: Xét tứ giác ABCE có
M là trung điểm chung của AC và BE
=>ABCE là hình bình hành
=>CE//AB
c: Xét ΔHAB vuông tại H và ΔHKC vuông tại H có
HB=HC
góc HAB=góc HKC
=>ΔHAB=ΔHKC
=>HA=HK
Xét tứ giác ABKC có
H là trung điểm chung của BC và AK
AB=AC
=>ABKC là hình thoi
=>AC=CK
Xét ΔABC có
BM,AH là trung tuyến
BM cắt AH tại G
=>G là trọng tâm
=>3GH=AH
3GH+HC=AH+HC>AC=CK
CM
4 tháng 1 2019
+) Xét tam giác EIA vuông tại I nên :
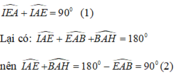
+) Xét hai tam giác ABH và ∆EAI có:
AB = AE ( vì ABDE là hình vuông)
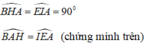
Suy ra: ∆ABH = ∆ EAI ( cạnh huyền – góc nhọn)
⇒ AH = EI ( hai cạnh tương ứng)
+) Tương tự hai tam giác vuông ACH và GAJ bằng nhau.
⇒ AH = GJ.
Suy ra EI = AH = GJ.
+) Xét ΔEKI và ΔGKJ có:
EI = GJ ( chứng minh trên)
∠(IKE) = ∠(JKG) (đối đỉnh).
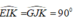
do đó ΔEKI = ΔGKJ ( cgv – gn)
suy ra: KE = KG
Từ đó ta có K trung điểm của EG. Vậy AK là trung tuyến của tam giác AEG.
14 tháng 4 2023
a;
có Abc là tam giac cân taji A (gt)
=> AH là đg cao và là ddg trùng tuyến và là đg phan giác
=> H là trung điểm của BC
Xét tam giác ABH va ACH có
1: có AH chung
2: HB=HC( CMT)
3: AB=AC (2 cạnh bên của tam giác ABC cân tại a)
=> 2 tam giác bằng nhau theo TH c.c.c
b;
xét 2 tam giác: AMB va CME có
AM=MC ( BM là trung tuyến=>m là trung điểm AC)
MB=ME (GT)
Góc AMB=Goc AMC (2 góc đối đỉnh)
=> 2tam giác bằng nhau theo TH (CGC)
=> góc CEm= góc ABM (2 góc tương ung trong 2 tam giác bằng nhau)
=> AB//CE (2 đg thằng có 2 góc đồng vị bằng nhau)
c;
có AB//CE (CMt)
=> Góc ABC= góc BCK (2 góc so le trong)
xet 2 tam giác vuông ACH va KCH có
HC chung
goc KCH=ACH (cùng bằng góc ABC)
=> 2 tam giác bằng nhau
=>HK=AH (1)
xet Tam gioác ABC có am là trung tuyên tại M; BM là trung tuyến
=> G là trọng tâm
=> HG= 1/3 AH (tinh chât trọng tâm của tam giác) (2)
tù 1 và 2 => HG=1/3 HK => HK=3HG(3)
Trong Tam giác KHC có
CK< HC+HK (4)
Từ 3 và 4 => KC< HC+3HG (dieu phai chung minh)
30 tháng 4 2022
a: XétΔABH vuông tại H và ΔACH vuông tại H có
AB=AC
AH chung
Do đó: ΔABH=ΔACH
Suy ra: BH=CH
b: BH=CH=BC/2=18(cm)
nên AH=24(cm)
9 tháng 12 2023
a: Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
=>ABDC là hình bình hành
Ta có: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=6^2+8^2=100\)
=>\(BC=\sqrt{100}=10\left(cm\right)\)
Hình bình hành ABDC có \(\widehat{BAC}=90^0\)
nên ABDC là hình chữ nhật
=>AD=BC
mà BC=10cm
nên AD=10cm
b: Xét ΔMHA vuông tại H và ΔMKD vuông tại K có
MA=MD
\(\widehat{HMA}=\widehat{KMD}\)(hai góc đối đỉnh)
Do đó: ΔMHA=ΔMKD
=>MH=MK
=>M là trung điểm của HK
Xét tứ giác AHDK có
M là trung điểm chung của AD và HK
=>AHDK là hình bình hành
=>AK//DH
c: E đối xứng A qua BC
=>BC là đường trung trực của AE
=>BC\(\perp\)AE tại trung điểm của AE(1)
Ta có: BC\(\perp\)AE
BC\(\perp\)AH
AE,AH có điểm chung là A
Do đó: E,A,H thẳng hàng(2)
Từ (1) và (2) suy ra H là trung điểm của AE
Xét ΔADE có
H,M lần lượt là trung điểm của AE,AD
=>HM là đường trung bình của ΔADE
=>HM//DE
mà \(H\in BC;M\in\)BC
nên DE//BC
Xét ΔCAE có
CH là đường cao
CH là đường trung tuyến
Do đó: ΔCAE cân tại C
=>CA=CE
mà CA=BD(ABDC là hình chữ nhật)
nên CE=BD
Xét tứ giác BEDC có DE//BC
nên BEDC là hình thang
Hình thang BEDC có BD=CE
nên BEDC là hình thang cân
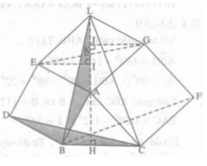
A B C a h k H M