cho tam giác abc có ab=ac = 10cm,bc = 12cm,các đường cao ad và ce cắt nhau tại h. a) tính ad b) tam giác abd đồng dạng với tam giác cbe c) tính be,hd
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
21 tháng 6 2023
a: Xét ΔABD vuông tại D và ΔCBE vuông tại E có
góc B chung
=>ΔABD đồng dạng với ΔCBE
b:
ΔABC cân tại A có AD là đường cao
nên D là trung điểm của BC
=>DB=DC=12/2=6cm
=>AD=8cm
ΔABD đồng dạng với ΔCBE
=>BE/BD=AB/CB=AD/CE
=>BE/6=10/12=8/CE
=>BE=5cm; CE=12*8/10=9,6cm
c: Xét ΔCDH vuông tại D và ΔCEB vuông tại E có
góc HCD chung
=>ΔCDH đồng dạng với ΔCEB
=>HD/EB=CD/CE
=>HD/5=6/9,6=5/8
=>HD=25/8cm
25 tháng 7 2022
a: Xét ΔBDH vuông tại D và ΔBEC vuông tại E có
góc DBH chung
Do đó: ΔBDH đồng dạng với ΔBEC
Xét ΔBDH vuông tại D và ΔAEH vuông tại E có
góc BHD=góc AHE
Do đó: ΔBDH đồng dạng với ΔAEH
b: DC=BC/2=60(cm)
=>AD=80cm
Xét ΔBEC vuông tại E và ΔADC vuông tại D có
góc C chung
Do đó: ΔBEC đồng dạng với ΔADC
=>BE/AD=EC/DC=BC/AC
=>BE/80=EC/60=120/100=6/5
=>BE=96(cm); EC=72(cm)
Ta có: ΔBDH đồng dạng với ΔBEC
nên BD/BE=DH/EC=BH/BC
=>DH/72=BH/120=60/96=5/8
=>DH=45cm; BH=75cm
Ta có;ΔBDH đồng dạng với ΔAEH
nên BD/AE=DH/EH=BH/AH
=>45/EH=75/AH=60/100-72=60/28=15/7
=>EH=45:15/7=45x7/15=21(cm)
3
7 tháng 4 2020
b) xét ∆ABC có AD là đường phân giác của góc A
=>BD/AB=DC/AC ( tính chất)
Áp dụng tính chất dãy tỉ số bằng nhau , được :
BD/AB=DC/AC=BD/6=DC/8=(BD+DC)/(6+8)=BD/14=10/14=5/7
==>BD=6×5:7≈4,3
==>DC=10-4,3≈5,7
3
7 tháng 4 2020
a,Áp dụng định lý Pi-ta-go vào tam giác ABC => tam giác ABC vuông tại A=> AH vuông góc vs BC
=> tam giác ABC đồng dạng vs tam giác HAC ( g.c.g)
b, Vì tam giác ABC vuông tại A nên ta có hệ thức: AC2=BC . HC => đpcm
c, có AD là tia phân giác của tam giác ABC => BD=CD=BC/2= 5cm
25 tháng 7 2022
a: Xét ΔBDH vuông tại D và ΔBEC vuông tại E có
góc DBH chung
Do đó: ΔBDH đồng dạng với ΔBEC
Xét ΔBDH vuông tại D và ΔAEH vuông tại E có
góc BHD=góc AHE
Do đó: ΔBDH đồng dạng với ΔAEH
b: DC=BC/2=60(cm)
=>AD=80cm
Xét ΔBEC vuông tại E và ΔADC vuông tại D có
góc C chung
Do đó: ΔBEC đồng dạng với ΔADC
=>BE/AD=EC/DC=BC/AC
=>BE/80=EC/60=120/100=6/5
=>BE=96(cm); EC=72(cm)
Ta có: ΔBDH đồng dạng với ΔBEC
nên BD/BE=DH/EC=BH/BC
=>DH/72=BH/120=60/96=5/8
=>DH=45cm; BH=75cm
Ta có;ΔBDH đồng dạng với ΔAEH
nên BD/AE=DH/EH=BH/AH
=>45/EH=75/AH=60/100-72=60/28=15/7
=>EH=45:15/7=45x7/15=21(cm)
9 tháng 5 2022
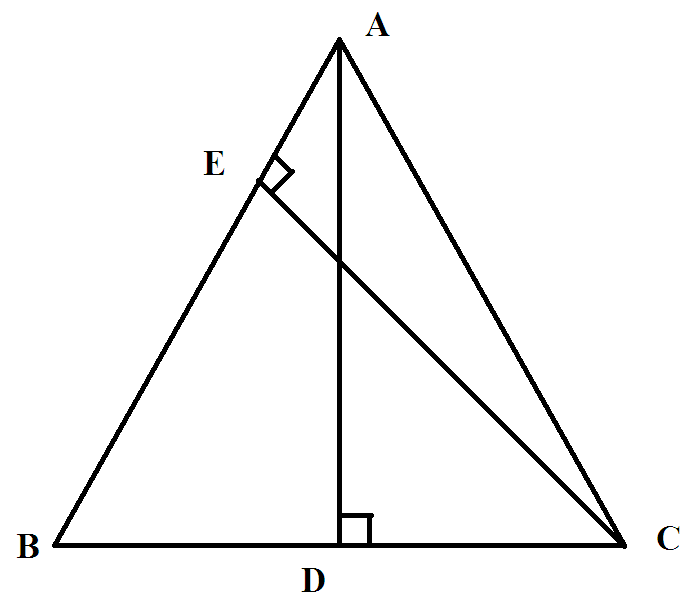
a) Xét △ABD và △CBE có:
\(\widehat{ADB}=\widehat{BEC}=90^o\)
\(\widehat{B}chung\)
Nên △ABD ∼ △CBE(g.g)
b)Theo câu a, ta có: △ABD ∼ △CB E
<=>\(\dfrac{AB}{BC}=\dfrac{BD}{BE}\Leftrightarrow AB.BE=BD.BC\)
c)Ta có:
\(BE=\dfrac{BD.BC}{AB}=\dfrac{3.12}{9}=4\left(cm\right)\)
5 tháng 3 2022
Áp dụng định lý phân giác ta có:
\(\dfrac{AD}{DC}=\dfrac{AB}{AC}=\dfrac{4}{5}\Rightarrow\dfrac{AD}{4}=\dfrac{DC}{5}=\dfrac{AD+DC}{4+5}=\dfrac{10}{9}\)
\(\dfrac{AD}{4}=\dfrac{10}{9}\Rightarrow AD=\dfrac{40}{9}\left(cm\right)\\ \dfrac{DC}{5}=\dfrac{10}{9}\Rightarrow DC=\dfrac{50}{9}\)
Áp dụng định lý phân giác ta có:
\(\dfrac{AE}{EB}=\dfrac{AC}{BC}=\dfrac{5}{6}\Rightarrow\dfrac{AE}{5}=\dfrac{EB}{6}=\dfrac{AE+EB}{5+6}=\dfrac{8}{11}\)
\(\dfrac{AE}{5}=\dfrac{8}{11}\Rightarrow AE=\dfrac{40}{11}\left(cm\right)\\ \dfrac{EB}{6}=\dfrac{8}{11}\Rightarrow EB=\dfrac{48}{11}\left(cm\right)\)
25 tháng 7 2022
a: Xét ΔBDH vuông tại D và ΔBEC vuông tại E có
góc DBH chung
Do đó: ΔBDH đồng dạng với ΔBEC
Xét ΔBDH vuông tại D và ΔAEH vuông tại E có
góc BHD=góc AHE
Do đó: ΔBDH đồng dạng với ΔAEH
b: DC=BC/2=60(cm)
=>AD=80cm
Xét ΔBEC vuông tại E và ΔADC vuông tại D có
góc C chung
Do đó: ΔBEC đồng dạng với ΔADC
=>BE/AD=EC/DC=BC/AC
=>BE/80=EC/60=120/100=6/5
=>BE=96(cm); EC=72(cm)
Ta có: ΔBDH đồng dạng với ΔBEC
nên BD/BE=DH/EC=BH/BC
=>DH/72=BH/120=60/96=5/8
=>DH=45cm; BH=75cm
Ta có;ΔBDH đồng dạng với ΔAEH
nên BD/AE=DH/EH=BH/AH
=>45/EH=75/AH=60/100-72=60/28=15/7
=>EH=45:15/7=45x7/15=21(cm)
b: Xét ΔABD vuông tại D và ΔCBE vuông tại E có
\(\widehat{B}\) chung
Do đó: ΔABD\(\sim\)ΔCBE
cau c nx
cau a minh bt r