Chứng tỏ x0 = 1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
16 tháng 1 2019
Câu a :))
Hàm số đã cho đồng biến .
giải thích :
Do \(m^2\ge0\forall m\)
\(\Rightarrow m^2+1>0\)
Vậy hàm số trên đồng biến.
NA
16 tháng 1 2019
Giả sử đths đi qua điểm cố định ( x0;y0 )
Ta có y0 = ( m2 +1 )x0 - 1
<=> y0 = m2 x0 +x0 -1
<=> y0 -x0 +1 -m2x0 = 0
Để pt nghiệm đúng với mọi m \(\Leftrightarrow\hept{\begin{cases}y_0-x_0+1=0\\x_0=0\end{cases}\Leftrightarrow\hept{\begin{cases}y_0=-1\\x_0=0\end{cases}}}\)
Vậy đths luôn đi qua điểm cố định ( 0 ; -1 )
CM
29 tháng 11 2017
- Xét hàm số f ( x ) = x 3 + x - 1 , ta có f(0) = -1 và f(1) = 1 nên: f(0).f(1) < 0.
- Mặt khác: f ( x ) = x 3 + x - 1 là hàm đa thức nên liên tục trên [0;1].
- Suy ra f ( x ) = x 3 + x - 1 đồng biến trên R nên phương trình x 3 + x - 1 = 0 có nghiệm duy nhất x 0 ∈ ( 0 ; 1 ) .
- Theo bất đẳng thức Côsi:
CM
26 tháng 10 2019
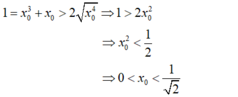
Đặt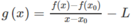 
Suy ra g(x) xác định trên
(
a
;
b
)
\
x
0
và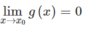 
Mặt khác, f ( x ) = f ( x 0 ) + L ( x − x 0 ) + ( x − x 0 ) g ( x ) nên
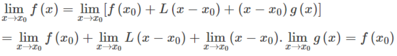
Vậy hàm số y = f(x) liên tục tại
BC
0
CM
27 tháng 1 2017
Chọn C.
Điều kiện. x ≠ -1
Phương trình tương đương 
Lấy ln hai vế của , ta được 
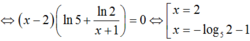
Suy ra x0 = 2 và P = 60.
TT
1
5 tháng 8 2017
Dễ thấy: \(x_0;y_0\ne 0\)
*)Xét \(x_0;y_0>0\) xài BĐT AM-GM
\(x^3+y^3+1\ge3\sqrt[3]{x^3y^3}=3xy\)
Xảy ra khi \(x=y=1\)
Khi đó \(\left(1+x_0\right)\left(1+\dfrac{1}{y_0}\right)\left(1+\dfrac{x_0}{y_0}\right)=8\)
*)Xét \(x_0;y_0<0\)\(\Rightarrow3xy>0;x^3+y^3+1\le0\) (loại)
CM
3 tháng 8 2019
Vì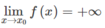 
nên với dãy số ( x n ) bất kì, x n ∈ K \ x 0 và x n → x 0 ta luôn có
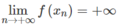
Từ định nghĩa suy ra f ( x n ) có thể lớn hơn một số dương bất kì, kể từ một số hạng nào đó trở đi.
Nếu số dương này là 1 thì f ( x n ) > 1 kể từ một số hạng nàođó trởđi.
Nói cách khác, luôn tồn tạiít nhất một số x k ∈ K \ x 0 sao cho f ( x k ) > 1 .
KV
22 tháng 10 2023
a) P = 1 + 3 + 3² + ... + 3¹⁰¹
= (1 + 3 + 3²) + (3³ + 3⁴ + 3⁵) + ... + (3⁹⁹ + 3¹⁰⁰ + 3¹⁰¹)
= 13 + 3³.(1 + 3 + 3²) + ... + 3⁹⁹.(1 + 3 + 3²)
= 13 + 3³.13 + ... + 3⁹⁹.13
= 13.(1 + 3³ + ... + 3⁹⁹) ⋮ 13
Vậy P ⋮ 13
b) B = 1 + 2² + 2⁴ + ... + 2²⁰²⁰
= (1 + 2² + 2⁴) + (2⁶ + 2⁸ + 2¹⁰) + ... + (2²⁰¹⁶ + 2²⁰¹⁸ + 2²⁰²⁰)
= 21 + 2⁶.(1 + 2² + 2⁴) + ... + 2²⁰¹⁶.(1 + 2² + 2⁴)
= 21 + 2⁶.21 + ... + 2²⁰¹⁶.21
= 21.(1 + 2⁶ + ... + 2²⁰¹⁶) ⋮ 21
Vậy B ⋮ 21
c) A = 2 + 2² + 2³ + ... + 2²⁰
= (2 + 2² + 2³ + 2⁴) + (2⁵ + 2⁶ + 2⁷ + 2⁸) + ... + (2¹⁷ + 2¹⁸ + 2¹⁹ + 2²⁰)
= 30 + 2⁴.(2 + 2² + 2³ + 2⁴) + ... + 2¹⁶.(2 + 2² + 2³ + 2⁴)
= 30 + 2⁴.30 + ... + 2¹⁶.30
= 30.(1 + 2⁴ + ... + 2¹⁶)
= 5.6.(1 + 2⁴ + ... + 2¹⁶) ⋮ 5
Vậy A ⋮ 5
d) A = 1 + 4 + 4² + ... + 4⁹⁸
= (1 + 4 + 4²) + (4³ + 4⁴ + 4⁵) + ... + (4⁹⁷ + 4⁹⁸ + 4⁹⁹)
= 21 + 4³.(1 + 4 + 4²) + ... + 4⁹⁷.(1 + 4 + 4²)
= 21 + 4³.21 + ... + 4⁹⁷.21
= 21.(1 + 4³ + ... + 4⁹⁷) ⋮ 21
Vậy A ⋮ 21
e) A = 11⁹ + 11⁸ + 11⁷ + ... + 11 + 1
= (11⁹ + 11⁸ + 11⁷ + 11⁶ + 11⁵) + (11⁴ + 11³ + 11² + 11 + 1)
= 11⁵.(11⁴ + 11³ + 11² + 11 + 1) + 16105
= 11⁵.16105 + 16105
= 16105.(11⁵ + 1)
= 5.3221.(11⁵ + 1) ⋮ 5
Vậy A ⋮ 5
CM
30 tháng 11 2017
Đáp án A
Phương pháp:
Dựa vào khái niệm cực trị và các kiến thức liên quan.
Cách giải:
(1) chỉ là điều kiện cần mà không là điều kiện đủ.
VD hàm số y = x3 có y' = 3x2 = 0 ⇔ x = 0. Tuy nhiên x = 0 không là điểm cực trị của hàm số.
(2) sai, khi f''(x0) = 0, ta không có kết luận về điểm x0 có là cực trị của hàm số hay không.
(3) hiển nhiên sai.
Vậy (1), (2), (3): sai; (4): đúng
\(x^0=1\)
Vì theo quy ước
-\(x^1=x\)
-\(x^0=1\)
nên \(x^0=1\)