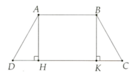
BT:cho hình thang cân ABCD(AB//CD) có AB=3cm,CD=6cm,AD=2.5cm.Vẽ 2 đường cao AH,BK.Tính DH,DK,AH
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NQ
3
NQ
4 tháng 8 2016
mog các bạn có tâm giúp tôi lm nhanh câu hỏi này
xin chân thành cảm ơn rất nhiều =)))
DN
5 tháng 7 2016
Hình ảnh chỉ mang tính chất minh họa
Ta có: AB=HK=3cm
=> DH=KC=(DC-HK):2=1,5cm
=> DK=DH+HK=4,5 cm
Theo định lí pitago trong tam giác vuông AHD có:
\(AH=\sqrt{AD^2-DH^2}=\sqrt{2,5^2-1,5^2}=2cm\)
Tương tự:
\(AK=\sqrt{AH^2+HK^2}=\sqrt{2^2+3^2}=\sqrt{13}cm\)
19 tháng 8 2021
Bài 8:
a: Xét ΔDBC có
E là trung điểm của BD
M là trung điểm của BC
Do đó: EM là đường trung bình của ΔDBC
Suy ra: EM//DC
b: Xét ΔAEM có
D là trung điểm của AE
DI//EM
Do đó: I là trung điểm của AM
19 tháng 8 2021
Bài 5:
Xét ΔABC có
\(\dfrac{AE}{EB}=\dfrac{AD}{DC}\left(=1\right)\)
Do đó: DE//BC
Xét tứ giác BEDC có DE//BC
nên BEDC là hình thang
mà \(\widehat{EBC}=\widehat{DCB}\)
nên BEDC là hình thang cân
CM
4 tháng 1 2020
a) Chứng minh
DADH = DBCK (ch-gnh)
Þ DH = CK
Vận dụng nhận xét hình thang ABKH (AB//KH) có AH//BK Þ AB = HK
b) Vậy D H = C D − A B 2
c) DH = 4cm, AH = 3cm; SABCD = 30cm2
Xet tam giác AHD và tam giác BKC có:
góc AHD = góc BKC ( = 90 độ)
AD=BC
góc ADH = góc BCK
=> tam giác AHD = tam giác BKC ( ch-gn)
=>AH = BK , DK = CK
Có : DH +HK + CK = DC
DH +3 +DH = 6
2 DH =3 DH = 1,5
=> DH = CK =1,5
Áp dụng định lí Pi- ta -go cho tam giác AHD ta có :
AH^2+HD^2 =AD^2 AH^2+1,5^2 =2,5^2 AH^2+2,25 =6,25 AH^2 =4
=>AH=2
Vậy DH =DK = 1,5 AH =2