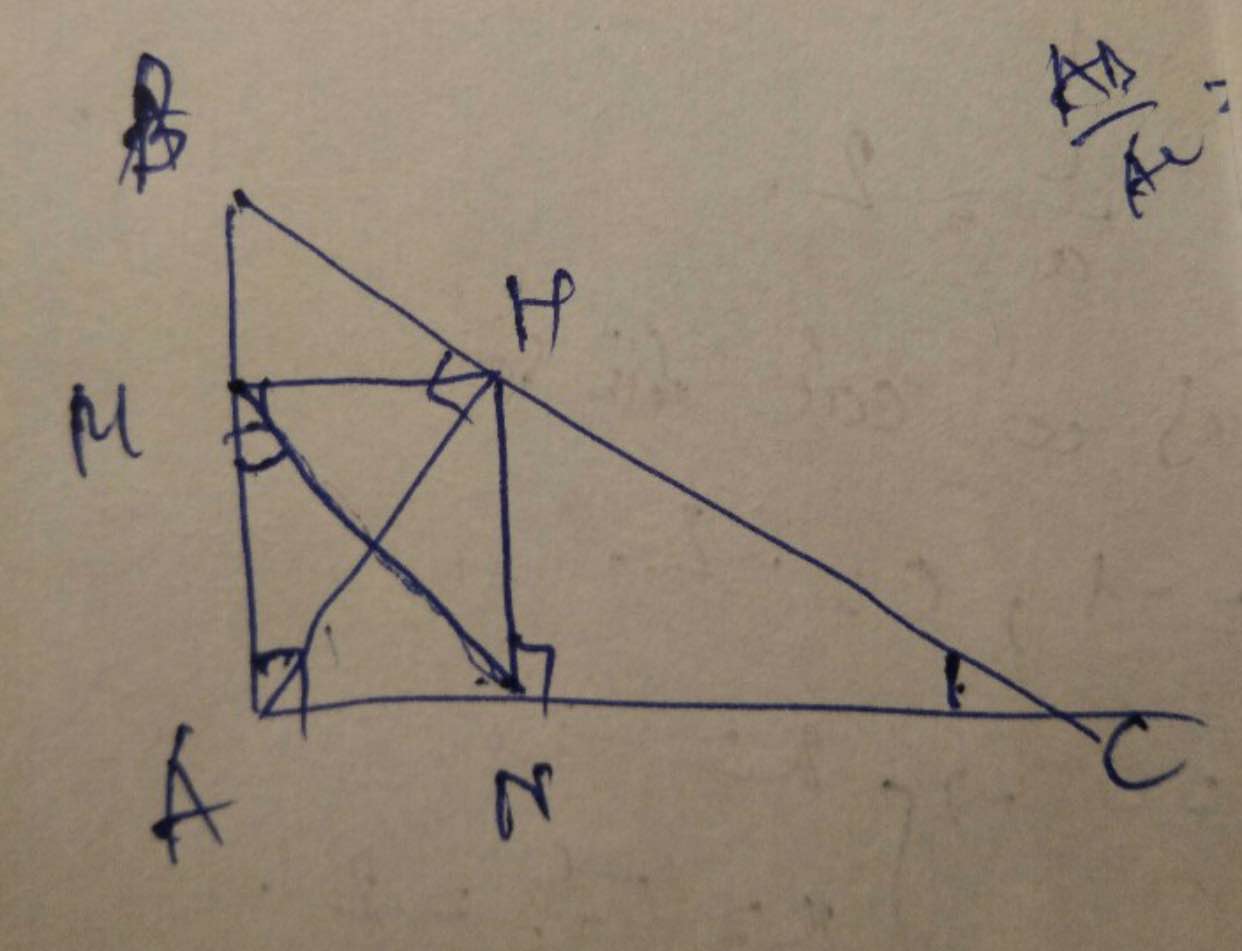
Cho tam giác ABC có Â vuông, đường cao AH.Gọi D,E lần lượt là hình chiếu của H trên AB,AC. Chúng minh rằng AB.AD=AC.AE=HB.HC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AT
15 tháng 7 2021
ý bạn là chứng minh \(\sqrt{HB.HC}=\sqrt[3]{BD.CE.BC}\)
tam giác ABC vuông tại A có AH là đường cao
\(\Rightarrow HB.HC=AH^2\Rightarrow\sqrt{HB.HC}=AH\)
Ta có: \(AH^4=\left(AH^2\right)^2=\left(BH.HC\right)^2=BH^2.CH^2\)
tam giác AHB vuông tại H có HD là đường cao \(\Rightarrow BH^2=BD.BA\)
tam giác AHC vuông tại H có HF là đường cao \(\Rightarrow CH^2=CE.CA\)
\(\Rightarrow BH^2.CH^2=BD.BA.CE.CA=BD.CE.\left(AB.AC\right)\)
tam giác ABC vuông tại A có AH là đường cao \(\Rightarrow AH.BC=AB.AC\)
\(\Rightarrow BD.CE.\left(AB.AC\right)=BD.CE.AH.BC\Rightarrow BD.CE.BC.AH=AH^4\)
\(\Rightarrow BD.CE.BC=AH^3\Rightarrow\sqrt[3]{BD.CE.BC}=AH\)
\(\Rightarrow\sqrt{HB.HC}=\sqrt[3]{BD.CE.BC}\)
31 tháng 10 2021
b: Xét ΔABC vuông tại A có AH là đường cao
nên \(HB\cdot HC=AH^2\left(1\right)\)
Xét ΔABH vuông tại H có HD là đường cao
nên \(AD\cdot AB=AH^2\left(2\right)\)
Xét ΔAHC vuông tại H có HE là đường cao
nên \(AE\cdot AC=AH^2\left(3\right)\)
Từ (1), (2) và (3) suy ra \(HB\cdot HC=AD\cdot AB=AE\cdot AC\)
20 tháng 7 2021
Ta có : \(AB^2=BH.BC\)
\(AC^2=CH.BC\)
Chia vế với vế ta được :
\(\dfrac{AB^2}{AC^2}=\dfrac{BH.BC}{CH.BC}\Rightarrow\dfrac{AB^2}{AC^2}=\dfrac{BH}{CH}\)
HH
15 tháng 4 2020
Ta có : ΔABC vuông tại A(gt)
AM là đường trung tuyến ứng với BC ( M là trung điểm BC )
⇒ AM = BM ( Tính chất đường trung tuyến ứng với cạnh huyền trong Δ vuông)
⇒ ΔAMB cân tại M
\(\Rightarrow\widehat{A_1}=\widehat{B}\left(1\right)\)
\(HI\perp AB\left(gt\right)\Rightarrow\widehat{HIA}=90^o\)
\(HK\perp AC\left(gt\right)\Rightarrow\widehat{HKA}=90^o\)
\(\widehat{A}=90^o\left(gt\right)\)
\(\Rightarrow AIHK\)có \(\widehat{A}=\widehat{HIA}=\widehat{HKA}=90^o\)
=> AIHK là hình CN ( dấu hiệu nhân biết )
Gọi N là giao điểm IK ; AH
=> NI = NA ( TÍnh chất hình chữ nhật) ⇒ ΔANI cân tại N
\(\Rightarrow\widehat{I_1}=\widehat{IAN}\left(3\right)\)Lại có \(\widehat{A_2}=\widehat{B}\)( cùng phụ với \(\widehat{C}\)) ( 2 )
Từ (1) và (2)
\(\Rightarrow\widehat{A_1}=\widehat{A}_2\left(4\right)\)Lại có : \(\widehat{IAN}+\widehat{A_2}=\widehat{A}=90^o\left(5\right)\)
Từ 3 ; 4 ; 5
\(\Rightarrow\widehat{I_1}+\widehat{A_1}=90^o\)mà \(\widehat{I_1}+\widehat{A_1}+\widehat{INA}=180^o\)
\(\Rightarrow90^o+\widehat{INA}=180^o\)
\(\Rightarrow\widehat{INA}=90^o\Rightarrow AM\perp IK\left(đpcm\right)\)
11 tháng 9 2018
cho tap hop A = { 1;2;3;4;.......;n} . Tìm số tự nhiên n biết tổng các phần tử của A bằng 90