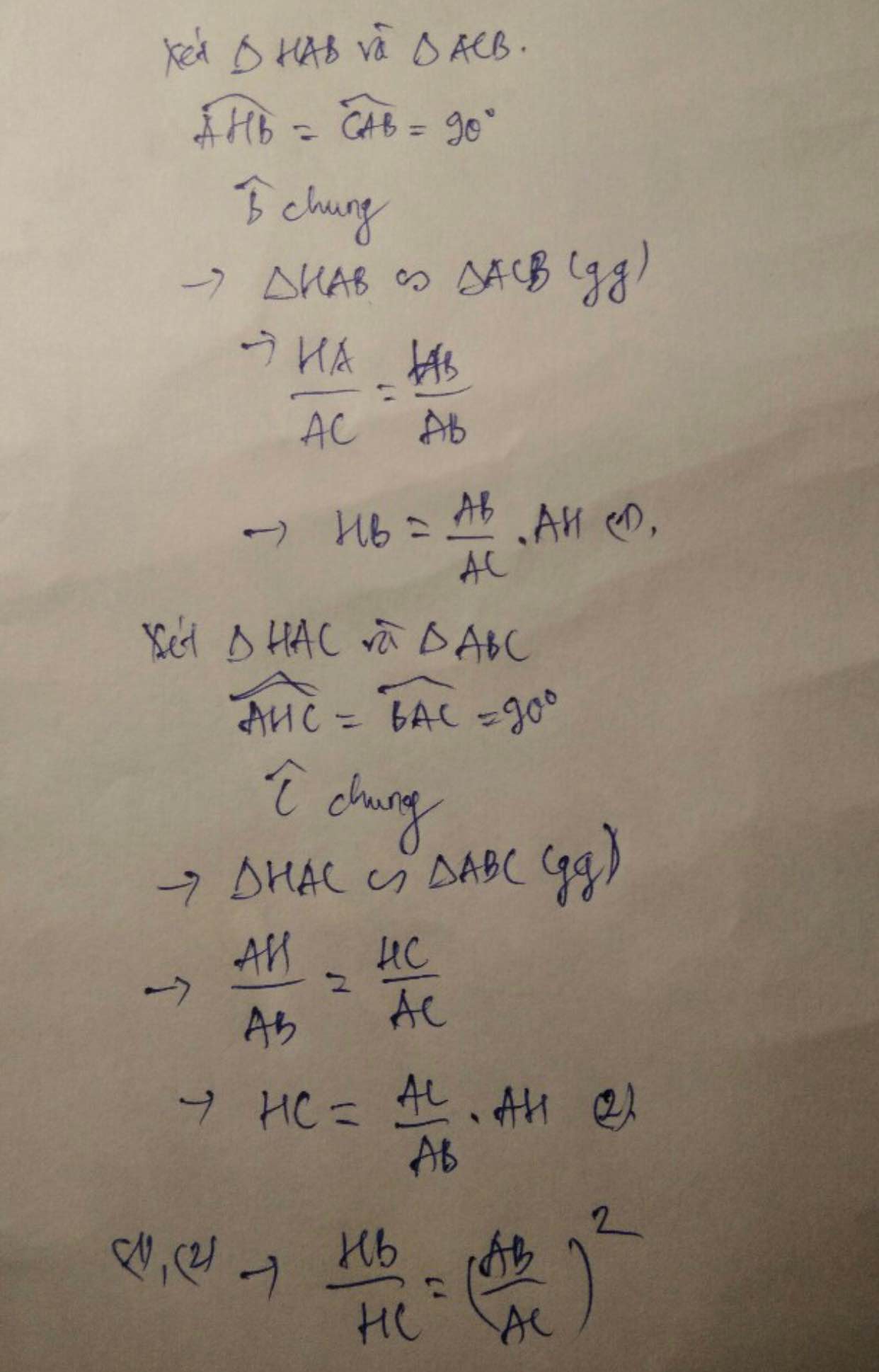Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ý bạn là chứng minh \(\sqrt{HB.HC}=\sqrt[3]{BD.CE.BC}\)
tam giác ABC vuông tại A có AH là đường cao
\(\Rightarrow HB.HC=AH^2\Rightarrow\sqrt{HB.HC}=AH\)
Ta có: \(AH^4=\left(AH^2\right)^2=\left(BH.HC\right)^2=BH^2.CH^2\)
tam giác AHB vuông tại H có HD là đường cao \(\Rightarrow BH^2=BD.BA\)
tam giác AHC vuông tại H có HF là đường cao \(\Rightarrow CH^2=CE.CA\)
\(\Rightarrow BH^2.CH^2=BD.BA.CE.CA=BD.CE.\left(AB.AC\right)\)
tam giác ABC vuông tại A có AH là đường cao \(\Rightarrow AH.BC=AB.AC\)
\(\Rightarrow BD.CE.\left(AB.AC\right)=BD.CE.AH.BC\Rightarrow BD.CE.BC.AH=AH^4\)
\(\Rightarrow BD.CE.BC=AH^3\Rightarrow\sqrt[3]{BD.CE.BC}=AH\)
\(\Rightarrow\sqrt{HB.HC}=\sqrt[3]{BD.CE.BC}\)

b: Xét ΔABC vuông tại A có AH là đường cao
nên \(HB\cdot HC=AH^2\left(1\right)\)
Xét ΔABH vuông tại H có HD là đường cao
nên \(AD\cdot AB=AH^2\left(2\right)\)
Xét ΔAHC vuông tại H có HE là đường cao
nên \(AE\cdot AC=AH^2\left(3\right)\)
Từ (1), (2) và (3) suy ra \(HB\cdot HC=AD\cdot AB=AE\cdot AC\)

Ta có : \(AB^2=BH.BC\)
\(AC^2=CH.BC\)
Chia vế với vế ta được :
\(\dfrac{AB^2}{AC^2}=\dfrac{BH.BC}{CH.BC}\Rightarrow\dfrac{AB^2}{AC^2}=\dfrac{BH}{CH}\)

cho tap hop A = { 1;2;3;4;.......;n} . Tìm số tự nhiên n biết tổng các phần tử của A bằng 90

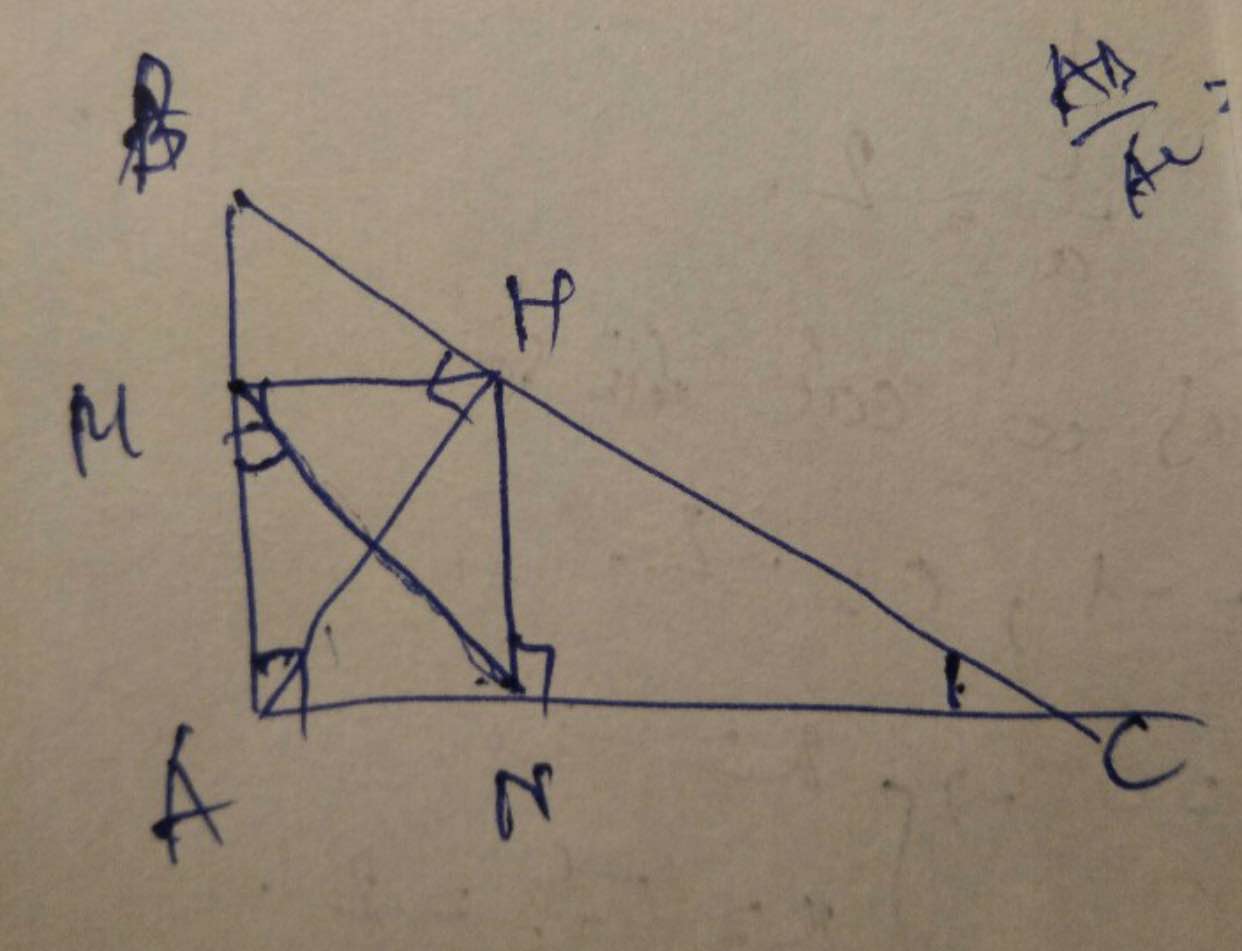
a, Xét tứ giác AMHN có : ^AMH = ^MAN = ^ANH = 900
Vậy tứ giác AMHN là hình chữ nhật
b, Ta có : \(AH^2=AM.AB\)( hệ thức lượng ) (1)
\(AH^2=AN.AC\)( hệ thức lượng ) (2)
Từ (1) ; (2) suy ra : \(AM.AB=AN.AC\Rightarrow\frac{AM}{AC}=\frac{AN}{AB}\)
Xét tam giác AMN và tam giác ACB ta có :
^A _ chung
\(\frac{AM}{AC}=\frac{AN}{AB}\)( cmt )
Vậy tam giác AMN ~ tam giác ACB ( c.g.c )
\(\Rightarrow\frac{AM}{AC}=\frac{MN}{BC}\)(3)
Theo định lí Pytago tam giác ABC vuông tại A
\(BC=\sqrt{AB^2+AC^2}=\sqrt{36+64}=10\)cm
Xét tam giác ABC vuông tại A, đường cao AH
* Áp dụng hệ thức : \(AH.BC=AB.AC\Rightarrow AH=\frac{AB.AC}{BC}=\frac{48}{10}=\frac{24}{5}\)cm
Lại có : \(AH^2=AM.AB\)( cmt ) \(\Rightarrow AM=\frac{AH^2}{AB}=\frac{96}{25}\)cm
\(\left(3\right)\Rightarrow\frac{AM}{AC}=\frac{MN}{BC}\Rightarrow MN=\frac{AM.BC}{AC}=\frac{24}{5}\)cm
c, Vì E là trung điểm BH mà tam giác BMH vuông tại M
=> ME là đường trung tuyến
=> \(ME=\frac{1}{2}BH\)(4)
Vì F là trung điểm HC mà tam giác HNC vuông tại N
=> NF là đường trung tuyến
=> \(NF=\frac{1}{2}HC\)(5)
Xét tam giác ABC vuông tại A, đường cao AH
* Áp dụng hệ thức : \(AB^2=BH.BC\Rightarrow BH=\frac{AB^2}{BC}=\frac{36}{10}=\frac{18}{5}\)cm (6)
=> \(HC=BC-HB=10-\frac{18}{5}=\frac{32}{5}\)cm (7)
Thay (6) vào (4) ta được : \(ME=\frac{1}{2}BH=\frac{1}{2}.\frac{18}{5}=\frac{18}{10}=\frac{9}{5}\)cm
Thay (7) vào (5) ta được : \(NF=\frac{1}{2}HC=\frac{1}{2}.\frac{32}{5}=\frac{32}{10}=\frac{16}{5}\)cm
d, mình chưa tìm ra dữ kiện