Làm b 203 giúp em vs ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
a. TXĐ: $\mathbb{R}$
Với $x\in\mathbb{R}$ thì $-x\in\mathbb{R}$
$f(x)=|x|=|-x|=f(-x)$
$\Rightarrow $ hàm chẵn
b. TXĐ: $\mathbb{R}$
Với $1\in\mathbb{R}$ thì $-1\in\mathbb{R}$
$f(1)=9; -f(1)=-9; f(-1)=1$
$\Rightarrow f(1)\neq f(-1); -f(1)\neq f(-1)$ nên hàm không chẵn không lẻ.
c.
TXĐ: $\mathbb{R}$
Với $x\in\mathbb{R}$ thì $-x\in\mathbb{R}$
$f(-x)=(-x)^3+(-x)=-(x^3+x)=-f(x)$ nên hàm lẻ
d.
TXĐ: $\mathbb{R}$
Với $1\in\mathbb{R}$ thì $-1\in\mathbb{R}$
$f(1)=3; f(-1)=1$
$\Rightarrow f(1)\neq f(-1); -f(1)\neq f(-1)$
Do đó hàm không chẵn không lẻ.


a) \(\left(2x-1\right)\left(x^2-x+1\right)+x^2\left(3-2x\right)=2\)
\(\Rightarrow2x^3-2x^2+2x-x^2+x-1+3x^2-2x^3=2\)
\(\Rightarrow\left(2x^3-2x^3\right)-\left(2x^2+x^2-3x^2\right)+\left(2x+x\right)-1=2\)
\(\Rightarrow3x-1=2\)
\(\Rightarrow3x=2-1\)
\(\Rightarrow3x=1\)
\(\Rightarrow x=\dfrac{1}{3}\)

19
Từ pt đầu ta có:
\(x^2-xy-2xy+2y^2=0\)
\(\Leftrightarrow x\left(x-y\right)-2y\left(x-y\right)=0\)
\(\Leftrightarrow\left(x-y\right)\left(x-2y\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=y\\x=2y\end{matrix}\right.\)
TH1: \(x=y\) thế xuống pt dưới:
\(y^2-y-y^2=1\Rightarrow y=-1\Rightarrow x=-1\)
TH2: \(x=2y\) thế xuống pt dưới:
\(\left(2y\right)^2-2y-y^2=1\Leftrightarrow3y^2-2y-1=0\)
\(\Rightarrow\left[{}\begin{matrix}y=1\Rightarrow x=2\\y=-\dfrac{1}{3}\Rightarrow x=-\dfrac{2}{3}\end{matrix}\right.\)
Vậy nghiệm của hệ là: \(\left(x;y\right)=\left(-1;-1\right);\left(1;2\right);\left(-\dfrac{1}{3};-\dfrac{2}{3}\right)\)
21.
Từ pt đầu:
\(xy+2=2x+y\Leftrightarrow xy-y+2-2x=0\)
\(\Leftrightarrow y\left(x-1\right)-2\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(y-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\y=2\end{matrix}\right.\)
TH1: \(x=1\) thế xuống pt dưới:
\(2y+y^2+3y=6\Leftrightarrow y^2+5y-6=0\)
\(\Rightarrow\left[{}\begin{matrix}y=1\\y=-6\end{matrix}\right.\)
TH2: \(y=2\) thế xuông pt dưới
\(4x+4+6=6\Rightarrow x=-1\)
Vậy nghiệm của pt là: \(\left(x;y\right)=\left(1;1\right);\left(1;-6\right);\left(-1;2\right)\)

a: Ta có: \(\left(\dfrac{3}{5}-\dfrac{7}{4}\right):\dfrac{23}{10}\)
\(=\dfrac{12-35}{20}\cdot\dfrac{10}{23}\)
\(=\dfrac{-23\cdot10}{23\cdot20}=-\dfrac{1}{2}\)
b: Ta có: \(\left(-\dfrac{2}{3}+\dfrac{3}{4}\right)^2\cdot\dfrac{12}{5}-\dfrac{11}{5}\)
\(=\dfrac{1}{144}\cdot\dfrac{12}{5}-\dfrac{11}{5}\)
\(=\dfrac{1}{60}-\dfrac{11}{5}=\dfrac{1}{60}-\dfrac{132}{60}=\dfrac{-131}{60}\)

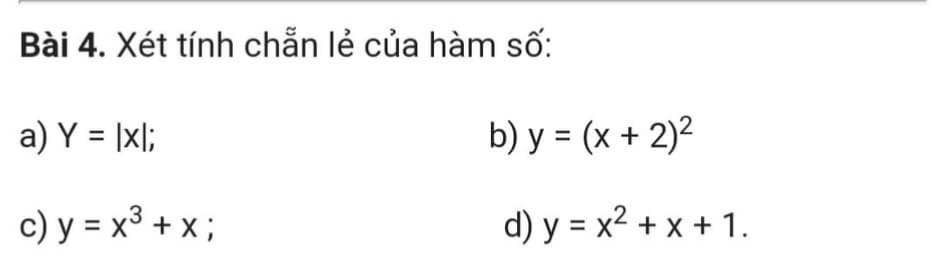



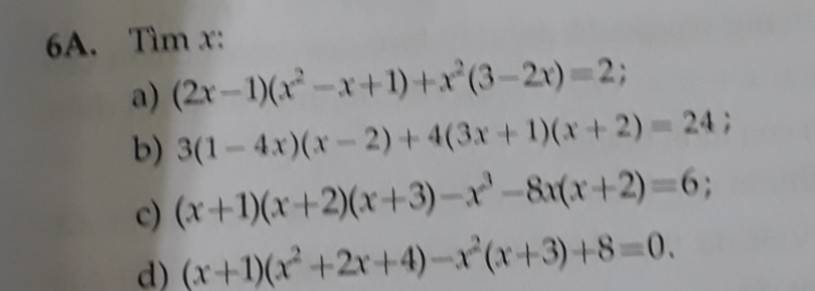 giúp em làm vs ạ
giúp em làm vs ạ

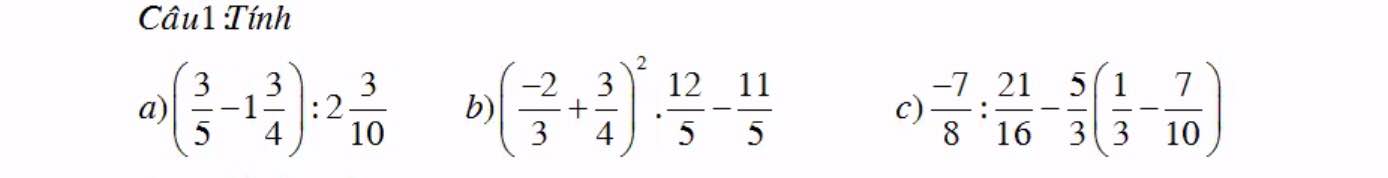

Em tách ra đăng từng bài một nha