Cho\(\Delta ABC=\Delta DEF\) , M là một điểm nằm trong tam giác, chứng minh rằng BMC=Â+ABM+ACM
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
3 tháng 8 2021
a)Từ A kẻ đường thẳng đi qua M cắt BC tại H
Ta có:\(\widehat{BAM}+\widehat{ABM}=\widehat{BHM}\) (tính chất góc ngoài của ΔABM)
Ta có:\(\widehat{MAC}+\widehat{ACM}=\widehat{CMH}\) (tính chất góc ngoài của ΔACM)
\(\Rightarrow\widehat{BAM}+\widehat{ABM}+\widehat{MAC}+\widehat{ACM}=\widehat{CMH}+\widehat{BHM}\)
\(\Leftrightarrow\widehat{BAC}+\widehat{ABM}+\widehat{ACM}=\widehat{BMC}\left(đpcm\right)\)
N
0
NN
1
17 tháng 9 2020
Xét tam giác ABC: \(\widehat{ABC}+\widehat{BAC}+\widehat{BCA}=180\Rightarrow\widehat{BAC}=180-\widehat{BCA}-\widehat{ABC}\)
\(=180-\left(\widehat{BCM}+\widehat{ACM}\right)-\left(\widehat{ABM}+\widehat{CBM}\right)\)
\(\Leftrightarrow\widehat{BAC}+\widehat{ABM}+\widehat{ACM}=180-\widehat{BCM}-\widehat{CBM}\)
Xét tam giác BMC: \(\widehat{BMC}+\widehat{CBM}+\widehat{BCM}=180\Leftrightarrow\widehat{BMC}=180-\widehat{BCM}-\widehat{CBM}\)
Vậy \(\widehat{BMC}=\widehat{BAC}+\widehat{ABM}+\widehat{ACM}\)
AH
Akai Haruma
Giáo viên
28 tháng 12 2023
Lời giải:
a.
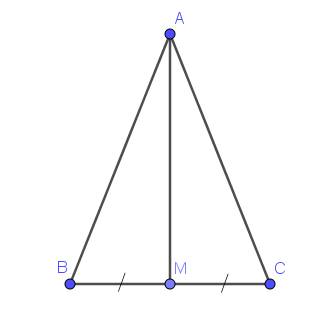
Do tam giác $ABC$ cân tại $A$ nên $AB=AC$
Xét tam giác $ABM$ và $ACM$ có:
$AB=AC$
$AM$ chung
$BM=CM$ (do $M$ là trung điểm $BC$)
$\Rightarrow \triangle ABM=\triangle ACM$ (c.c.c)
b.
Từ tam giác bằng nhau phần a suy ra $\widehat{BAM}=\widehat{CAM}$. Mà $AM$ nằm giữa $AB, AC$ nên $AM$ là tia phân giác $\widehat{BAC}$
Cũng từ tam giác bằng nhau phần a suy ra:
$\widehat{AMB}=\widehat{AMC}$
Mà $\widehat{AMB}+\widehat{AMC}=\widehat{BMC}=180^0$
$\Rightarrow \widehat{AMB}=180^0:2=90^0$
$\Rightarrow AM\perp BC$
c.
$AM\perp BC, M$ là trung điểm $BC$ nên $AM$ là đường trung trực của $BC$
$\Rightarrow$ mọi điểm $E\in AM$ đều cách đều 2 đầu mút B,C (theo tính chất đường trung trực)
$\Rightarrow EB=EC$
$\Rightarrow \triangle EBC$ cân tại $E$.
VT
1
30 tháng 6 2017
a, Xét tam giác ABC có:
BAC + (ABC + ACB)=1800
Xét tam giác MBC có:
BMC + (MCB + MBC)=1800
\(\Rightarrow\)BAC + (ABC + ACB) = BMC + (MCB + MBC) (1)
Vì M nằm trong tam giác ABC nên BM nằm giữa 2 tia BC và BA.
\(\Rightarrow\) ABC > MBC
Tương tự ta được: ACB > MCB.
\(\Rightarrow\)ABC + ACB > MBC + MCB (2)
Từ (1) và (2) suy ra: BAC < BMC.
b, Kéo dài AM, cắt BC tại E.
Xét tam giác ABM có BME là góc ngoài tại đỉnh M nên ta có:
BME = MAB + MBA. (1)
Tương tự đối với tam giác AMC có CME là góc ngoài tại đỉnh M nên ta cũng có:
CME = MAC + MCA. (2)
Từ (1) và (2) suy ra:
BME+CME = MAB + MBA + MAC + MCA.
\(\Rightarrow\)BMC = BAC + ABM + ACM
Sorry bn, mk ko gõ đc dấu mũ nha
22 tháng 12 2021
a: Xét ΔABM và ΔACM có
AB=AC
\(\widehat{BAM}=\widehat{CAM}\)
AM chung
Do đó: ΔABM=ΔACM