Tìm điều kiện để căn thức sau xác định \(\sqrt{x^2+5x+4}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Biểu thức trong căn thức \(\sqrt{\frac{3x+1}{10}}\)phải lớn hơn hoặc bằng 0
Căn thức có nghĩa\(\Leftrightarrow3x+1\ge0\Leftrightarrow x\ge\frac{-1}{3}\)

a )
\(\sqrt{\frac{3}{4}-5x}\ge0\)
\(< =>\frac{3}{4}-5x\ge0\)
\(< =>-5x\ge-\frac{3}{4}\)
\(< =>\frac{-20x}{4}\ge-\frac{3}{4}\)
\(< =>-20x\ge-3\)
\(< =>x\ge\frac{3}{20}\)
\(\sqrt{\frac{-3}{1}-2x}\ge0\)
\(< =>-3-2x\ge0\)
\(< =>-2x\ge3\)
\(< =>x\ge-\frac{3}{2}\)

a) \(\sqrt{3x-4}\) xác định \(\Leftrightarrow3x-4\ge0\Leftrightarrow3x\ge4\Leftrightarrow x\ge\dfrac{4}{3}\)
b) \(\dfrac{1}{\sqrt{x-4}}\) xác định \(\Leftrightarrow x-4>0\Leftrightarrow x>4\)

ĐKXĐ: `{(5x-1>=0),(x+2>=0),(7-x>=0):}`
`<=>{(x>=1/5),(x>=-2),(x<=7):}`
`<=>1/5 <=x<=7`
`ĐKXĐ: {(5x - 1 >= 0),(x+2 >=0),(7-x >=0):}`
`<=> {(x >= 1/5),(x>= -2),(x <=7):}`
`<=> 1/5 <= x <= 7`

a: ĐKXĐ: \(\dfrac{x-1}{5-x}\ge0\)
\(\Leftrightarrow\dfrac{x-1}{x-5}\le0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-1\ge0\\x-5< 0\end{matrix}\right.\Leftrightarrow1\le x< 5\)
b: ĐKXĐ: \(\left[{}\begin{matrix}x>3\\x< 2\end{matrix}\right.\)

Để \(\sqrt{\frac{x+3}{7-x}}\)có nghĩa thì x + 3 và 7 - x cùng dấu
\(TH1:\hept{\begin{cases}x+3\ge0\\7-x>0\end{cases}}\Rightarrow\hept{\begin{cases}x\ge-3\\x< 7\end{cases}}\Rightarrow-3\le x< 7\)(Vì x = 7 thì bt không có nghĩa)
\(TH2:\hept{\begin{cases}x+3\le0\\7-x< 0\end{cases}}\Rightarrow\hept{\begin{cases}x\le-3\\x>7\end{cases}}\left(L\right)\)
Vậy \(-3\le x< 7\)

a) ĐK: x ≥ 2
\(\sqrt{3x-6}=3\)
\(\Leftrightarrow3x-6=9\)
<=> 3x = 15
<=> x = 5
Vậy:....
b) ĐK: 5x - 16 ≥ 0
<=> 5x ≥ 16
<=> x ≥ 16/5
\(\sqrt{5x-16}=2\)
<=> 5x - 16 = 4
<=> 5x = 20
<=> x = 4
c) ĐK: \(x^2-4x+3\ne0\)
\(\Leftrightarrow\left(x-1\right)\left(x-3\right)\ne0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ne1\\x\ne3\end{matrix}\right.\)
bình phương hai vế ta được:
a)điều kiện của x:x≥2
3x-6=9 <=> x=5(nhận)
b)ĐK: x≥16/5
5x-16=4 <=>x=4(nhận)
c) ta có: \(\dfrac{2x-3}{\left(x-2\right)^2-1}\)= \(\dfrac{2x-3}{\left(x-3\right)\left(x-1\right)}\)
ĐKXĐ: x≠3 ;x≠1

Giá trị của biểu thức xác định khi mỗi giá trị của phân thức trong biểu thức đều được xác định.
Khi đó điều kiện xác định:
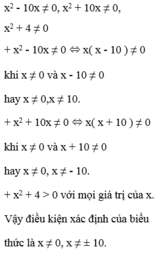
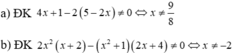
Căn thức xác định \(\Leftrightarrow x^2+5x+4\ge0\)
\(\Leftrightarrow\left(x+1\right)\left(x+4\right)\ge0\)
Do đó: (x+1) và (x+4) là 2 số cùng dấu.
TH1: \(\hept{\begin{cases}x+1\ge0\\x+4\ge0\end{cases}\Leftrightarrow\hept{\begin{cases}x\ge-1\\x\ge-4\end{cases}\Leftrightarrow}x\ge-1}\)
TH2: \(\hept{\begin{cases}x+1\le0\\x+4\le0\end{cases}\Leftrightarrow\hept{\begin{cases}x\le-1\\x\le-4\end{cases}\Leftrightarrow}x\le-4}\)
Vậy \(\orbr{\begin{cases}x\ge-1\\x\le-4\end{cases}}\)
Chúc bạn học tốt.