Chứng tò rằng 2110 chia hết cho 200
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


* Áp dụng hằng đẳng thức:
![]()
Ta có:
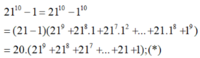
Ta có:
![]()
![]()
gồm có 10 số hạng
![]()
có chữ số tận cùng bằng 0. Do đó, ta có thể viết:
![]()
Thay vào (*) ta được:
2110 - 1 = 20.10.A = 200A
Suy ra: 2110 - 1 chia hết cho 200.

link tham khảo
ccaau hỏi của ng duy mạnh
link : https://olm.vn/hoi-dap/detail/60197622644.html
hok tót

Theo bài ra ta có:
abba = ax1000+bx100+bx10+a
=(ax1000+a)+(bx100+bx10)
=ax(1000+1)+bx(100+10)
=ax1001+bx111
Vì 1001 chia hết cho 11=>ax1001 chia hết cho 11(1)
Vì 111 chia hết cho 11=>bx111 chia hết cho 11(2)
Từ 1 và 2=>abba luôn chia hết cho 11


1993 - 199 = 199 ( 1992 - 1 ) = 199 ( 199 + 1 ) ( 199 - 1 ) = 199 . 198 . 200
=> 1993 - 199 chia hết cho 200

\(21^{10}-1\)
\(=\left(20+1\right)^{10}-1\)
\(=20^{10}+1^{10}-1\)
\(=20^{10}+\left(1-1\right)\)
\(=\left(20^2\right)^5\)
\(=400^5\)
\(=\left(200.2\right)^5\)
\(=200^5.2^5⋮200\left(đpcm\right)\)
21^10 -1
=(21^5)^2-1^2
=(21^5+1)(21^5-1)
Có 21^5+1=B suy rađặt 21^5+1=2k
suy ra 21^10=2k(21^5-1)=2k


Ta có:
\(742^3-692^3=\left(742-692\right)\left(742^2+742.692+692^2\right)=50.\left(742^2+742.692+692^2\right)\)
Do \(742⋮2\Rightarrow742^2⋮4\)
\(\left\{{}\begin{matrix}742⋮2\\692⋮2\end{matrix}\right.\) \(\Rightarrow742.692⋮4\)
\(692⋮2\Rightarrow692^2⋮4\)
\(\Rightarrow\left(742^2+742.692+692^2\right)⋮4\)
\(\Rightarrow\left(742^3-692^3\right)⋮\left(50.4=200\right)\) (đpcm)