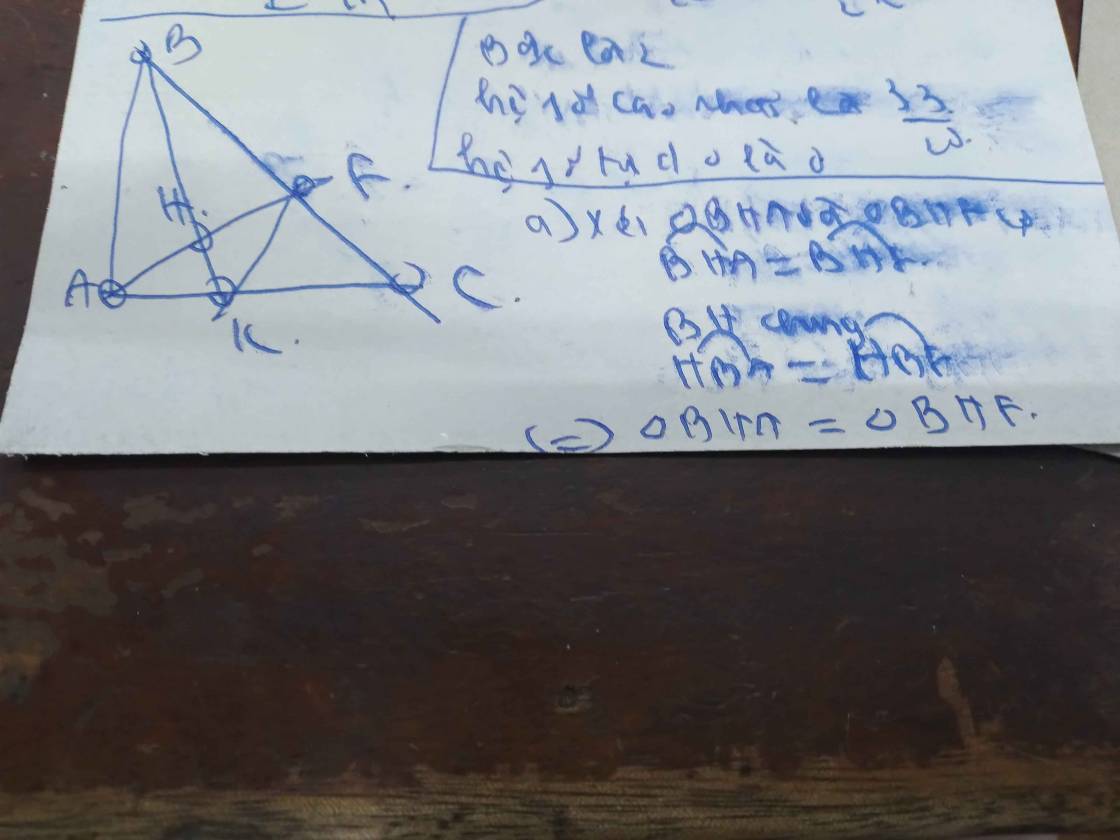
Chứng minh C vuông góc với B
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
8 tháng 7 2023
a: góc B+góc C=90 độ
góc HAC+góc C=90 độ
=>góc B=góc HAC
=>góc C=góc BAH
b: góc CAD+góc BAD=90 độ
góc CDA+góc HAD=90 độ
mà góc BAD=góc HAD
nên góc CAD=góc CDA
c: ΔCAD cân tại C có CK là phân giác
nên CK vuông góc AD
22 tháng 6 2023
a: Xét ΔOHC vuông tại H và ΔOKC vuông tại K có
OC chung
góc HOC=góc KOC
=>ΔOHC=ΔOKC
b: ΔOHC=ΔOKC
=>HO=KO
=>ΔOKH cân tại O
c: ΔOHK cân tại O
mà OM là phân giác
nên OM vuông góc HK
d: Xét ΔOHA vuông tại H và ΔOKB vuông tại K có
OH=OK
góc HOA chung
=>ΔOHA=ΔOKB
=>OA=OB
Xét ΔOAB có OH/OB=OK/OA
nên HK//AB
Q
21 tháng 11 2017
A B C 50* H K
a) Ta có \(\widehat{A}+\widehat{B}+\widehat{C}\) = 180o ( định lý tổng 3 góc của 1 tam giác )
90o+50o+\(\widehat{C}\) = 180o
140o+\(\widehat{C}\) = 180o
\(\widehat{C}\) = 180o-140o
\(\widehat{C}\) = 40o
b) Vì KH//AC có góc đồng vị tạo thành
Có \(\widehat{BKH}\) đồng vị với \(\widehat{BAC}\)
=> \(\widehat{BKH}\)=\(\widehat{BAC}\)=90o
=> HK vuông góc với AB
c) Ta có góc C = 40o (câu a)
Ta lại có : \(\widehat{HBK}+\widehat{BKH}+\widehat{BHK}=180^o\) (định lý tổng 3 góc của 1 tam giác)
50o+90o+\(\widehat{BHK}\) = 180o
\(\widehat{BHK}\) = 180o-(50o+90o)
=> \(\widehat{BHK}\) = 40o
Vậy góc BHK = góc C ( 40o=40o )
+ AH _|_ BC => \(\widehat{AHB}\) = 90o
Ta có \(\widehat{AHB}+\widehat{B}+\widehat{BAH}\) = 180o (định lý tổng 3 góc của 1 tam giác)
90o+50o+\(\widehat{AHB}\) = 180o
\(\widehat{AHB}\) = 180o-(90o+50o)
=> \(\widehat{AHB}\) = 40o
Vậy \(\widehat{KHB}=\)\(\widehat{AHB}\) (40o=40o)
23 tháng 2 2022
a, Xét tam giác ABC cân tại A có AM là đường cao
đồng thời là đường phân giác
Xét tam giác AMH và tam giác AMK
AM _ chung
^MAH = ^MAK ( AM là phân giác )
Vậy tam giác AMH = tam giác AMK ( ch - gn )
=> AH = AK ( 2 cạnh tương ứng )
b, Ta có AH = AK ; AB = AC
=> HK // BC ( Ta lét đảo )
23 tháng 2 2022
Xét \(\Delta AHM,\Delta AKM\) có:
\(\widehat{AHM}=\widehat{AKM}=90^o\)
\(\widehat{A_1}=\widehat{A_2}\)
\(AM:chung\)
\(\Rightarrow\Delta AHM=\Delta AKM\left(ch.gn\right)\)
\(\Rightarrow AH=AK\)
\(\Rightarrow\Delta AHK\) cân tại A
\(\Rightarrow\widehat{AHK}=\dfrac{180^o-\widehat{A}}{2}\left(1\right)\)
Vì \(\Delta ABC\) cân tại A
\(\Rightarrow\widehat{ABC}=\dfrac{180^o-\widehat{A}}{2}\left(2\right)\)
Từ (1) và (2) suy ra \(\widehat{AHK}=\widehat{ABC}\)
Mà 2 góc này ở vị trí đồng vị
Suy ra \(HK//BC\)
5 tháng 2 2022
a: Ta có: ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC
hay HB=HC
b: Ta có: ΔABC cân tại A
mà AH là đường cao
nên AH là đường phân giác
hay \(\widehat{BAH}=\widehat{CAH}\)
c: Xét ΔADH vuông tại D và ΔAEH vuông tại E có
AH chung
\(\widehat{DAH}=\widehat{EAH}\)
Do đó: ΔADH=ΔAEH
Suy ra: HD=HE
hay ΔHDE cân tại H
21 tháng 1 2024
a: Ta có: BE\(\perp\)DC
AC\(\perp\)DC
Do đó: BE//AC
Xét ΔDAC có ME//AC
nên \(\dfrac{DM}{DA}=\dfrac{DE}{DC}\)
b: Ta có: NE\(\perp\)BD
BC\(\perp\)BD
Do đó: NE//BC
Xét ΔDBC có NE//BC
nên \(\dfrac{DE}{DC}=\dfrac{DN}{DB}\)
=>\(\dfrac{DN}{DB}=\dfrac{DM}{DA}\)
Xét ΔDBA có \(\dfrac{DN}{DB}=\dfrac{DM}{DA}\)
nên MN//AB