Cho biểu thức:
M = \(\left(\dfrac{\sqrt{a}+1}{\sqrt{a}-1}+\dfrac{1-\sqrt{a}}{\sqrt{a}+1}\right):\left(\dfrac{\sqrt{a}+1}{\sqrt{a}-1}+\dfrac{\sqrt{a}}{\sqrt{a}+1}+\dfrac{\sqrt{a}}{1-a}\right)\)
a) Rút gọn M
b) Tính M khi a = 1 - \(\dfrac{\sqrt{3}}{2}\)
c) So sánh M với 2



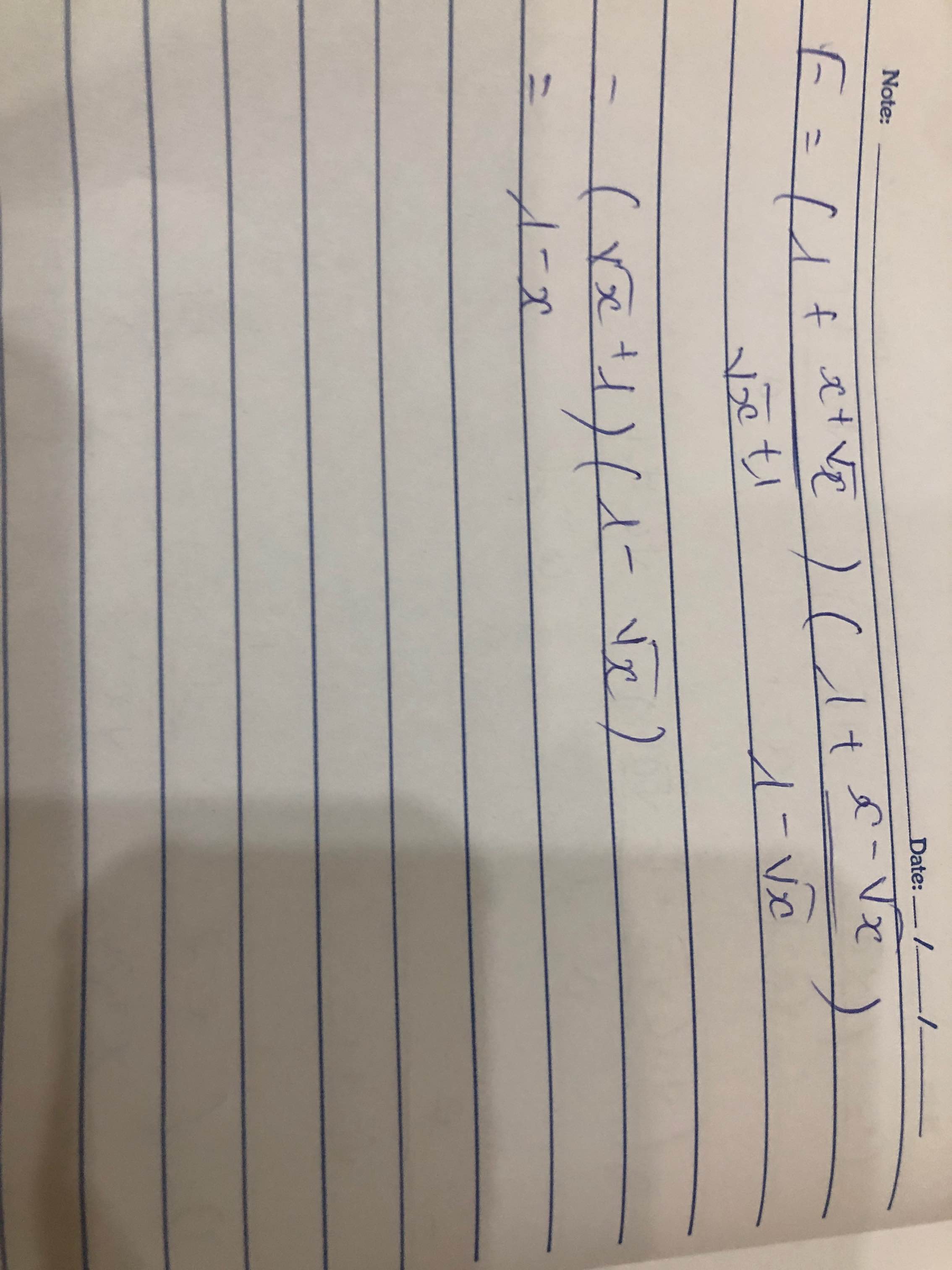
a. \(M=\left(\dfrac{\sqrt{a}+1}{\sqrt{a}-1}+\dfrac{1-\sqrt{a}}{\sqrt{a}+1}\right):\left(\dfrac{\sqrt{a}+1}{\sqrt{a}-1}+\dfrac{\sqrt{a}}{\sqrt{a}+1}+\dfrac{\sqrt{a}}{1-a}\right)\)
\(=\left(\dfrac{\left(\sqrt{a}+1\right)^2}{a-1}-\dfrac{\left(\sqrt{a}-1\right)^2}{a-1}\right):\left(\dfrac{\left(\sqrt{a}+1\right)^2}{a-1}+\dfrac{\sqrt{a}\left(\sqrt{a}+1\right)^2}{a-1}-\dfrac{\sqrt{a}}{a-1}\right)\)\(=\dfrac{\left(\sqrt{a}+1\right)^2-\left(\sqrt{a}-1\right)^2}{a-1}:\dfrac{\left(\sqrt{a}+1\right)^2+\sqrt{a}\left(\sqrt{a}-1\right)-\sqrt{a}}{a-1}\)
\(=\dfrac{\left(a+2\sqrt{a}+1\right)-\left(a-2\sqrt{a}+1\right)}{a-1}:\dfrac{\left(a+2\sqrt{a}+1\right)+a-\sqrt{a}-\sqrt{a}}{a-1}\)
\(=\dfrac{a+2\sqrt{a}+1-a+2\sqrt{a}-1}{a-1}:\dfrac{a+2\sqrt{a}+1+a-\sqrt{a}-\sqrt{a}}{a-1}\)
\(=\dfrac{4\sqrt{a}}{a-1}:\dfrac{2a+1}{a-1}\)
\(=\dfrac{4\sqrt{a}}{a-1}.\dfrac{a-1}{2a+1}\)
\(=\dfrac{4\sqrt{a}\left(a-1\right)}{\left(a-1\right)\left(2a+1\right)}\)
\(=\dfrac{4\sqrt{a}}{2a+1}\)