Hai đoạn thẳng AB và CD cắt nhau tại trung điểm của mỗi đoạn. Gọi E và F theo thứ tự trung điểm của các đoạn thẳng AD và BD. Các đoạn thẳng CE và CF lần lượt cắt đoạn thẳng AB tại I, J. Chứng minh rằng :
AI = IJ= JB
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
8 tháng 5 2018
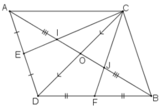
Gọi O là giao điểm của hai đoạn thẳng AB và CD.
⇒ AO = OB và CO = OD.
+ ΔACD có trung tuyến AO, CE cắt nhau tại I
⇒ I là trọng tâm ΔACD
⇒ AI = 2/3. AO = 2/3. 1/2. AB = 1/3.AB
+ Tương tự J là trọng tâm ΔBCD
⇒ BJ = 2/3. BO = 2/3. 1/2. BA = 1/3.AB
⇒ IJ = AB – AI – BJ = 1/3.AB
Vậy AI = IJ = JB
18 tháng 5 2022
Gọi O là giao điểm của AB và CD
=>O là trung điểm chng của AB và CD
Xét ΔACD có
AO là đường trung tuyến
CE là đường trung tuyến
AO cắt CE tại I
Do đó: I là trọng tâm
=>AI=2/3AO=1/3AB(1)
Xét ΔCBD có
BO là đường trung tuyến
CF là đường trung tuyến
BO cắt CF tại J
Do đó; J là trọng tâm
=>BJ=2/3BO=1/3BA(2)
Từ (1) và (2) suy ra AI=BJ=1/3AB=JI