giải tam giác vuông ABC,biết \(\widehat{A}\)=900 và:
a)a=15cm,b=10cm
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a, Sử dụng tỉ số cosC và sinC, tính được
a = 20 3 3 cm, c = 10 3 3 cm và B ^ = 60 0
b, Sử dụng tỉ số sinB và cosB, tính được:
b = 20.sin 35 0 ≈ 11,47cm, c = 20.cos 35 0 ≈ 16,38cm
c, Sử dụng định lý Pytago và tỉ số sinB, tính được:
c = 5 5 cm, sinB = 10 15 => B ^ ≈ 41 , 8 0 , C ^ ≈ 48 , 2 0
d, Tương tự c) ta có
a = 193 cm, tanB = 12 7 => B ^ ≈ 59 , 7 0 , C ^ = 30 , 3 0

a) Áp dụng HTL ta có:\(MH.HP=MH^2\Rightarrow x=\sqrt{2.8}=4\)
\(BC=MH+HP=10\)
Áp dụng HTL ta có: \(HP.NP=MP^2\Rightarrow y=\sqrt{8.10}=4\sqrt{5}\)
b) Áp dụng HTL ta có: \(EQ.QF=DQ^2\Rightarrow x=\dfrac{4^2}{1}=16\)
\(EF=EQ+QF=17\)
Áp dụng HTL ta có: \(QP.EF=y^2\Rightarrow y=\sqrt{17.1}=\sqrt{17}\)

* Trong tam giác vuông A’B’C’ có ∠ A ' = 90 0
Áp dụng định lí Pi-ta-go, ta có: A ' B ' 2 + A ' C ' 2 = B ' C ' 2
Suy ra: A ' C ' 2 = B ' C ' 2 - A ' B ' 2 = 15 2 - 9 2 = 144
Suy ra: A’C’ = 12 (cm)
* Trong tam giác vuông ABC có ∠ A = 90 0
Áp dụng định lí Pi-ta-go, ta có: B C 2 = A B 2 + A C 2 = 6 2 + 8 2 =100
Suy ra: BC = 10 (cm)
Ta có: 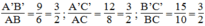
Suy ra: 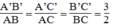
Vậy △ A’B’C’ đồng dạng ΔABC (c.c.c)

b: AB=10cm
\(BC=5\sqrt{3}\left(cm\right)\)
\(\widehat{C}=60^0\)

a) (H.a)
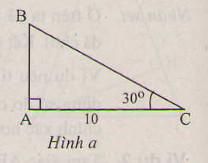
ˆB=90∘−30∘=60∘.B^=90∘−30∘=60∘.
AB=AC⋅tgC=10⋅tg30∘≈5,774(cm)AB=AC⋅tgC=10⋅tg30∘≈5,774(cm)
BC=ACcosC=10cos30∘≈11,547(cm)BC=ACcosC=10cos30∘≈11,547(cm).
b) (H.b)
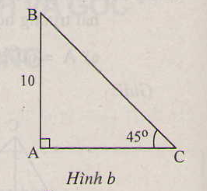
ˆB=90∘−45∘=45∘.B^=90∘−45∘=45∘.
⇒AC=AB=10(cm);⇒AC=AB=10(cm);
BC=ABsinC=10sin45∘≈14,142(cm)BC=ABsinC=10sin45∘≈14,142(cm)
c) (H.c)
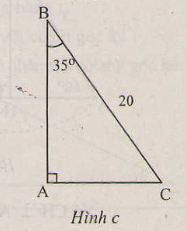
ˆC=90∘−35

a: Xét ΔABC vuông tại A và ΔDEF vuông tại D có
AB/DE=AC/DF
Do đó: ΔABC\(\sim\)ΔDEF
b: \(\dfrac{C_{ABC}}{C_{DEF}}=\dfrac{AB}{DE}=\dfrac{2}{3}\)

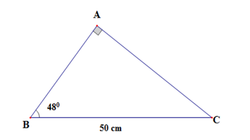
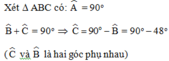
Áp dụng hệ thức liên hệ giữa cạnh và góc trong tam giác vuông ta có:
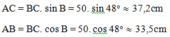
Vậy AC = 37,2cm; AB = 33,5cm; C ^ = 42 0
Đáp án cần chọn là: D
a: \(AC=10cm;BC=15cm\)
\(AB=\sqrt{15^2-10^2}=5\sqrt{5}\left(cm\right)\)
Xét ΔABC vuông tại A có sin B=AC/BC=2/3
nên góc B=42 độ
=>góc C=48 độ