Vẽ 5 đường thẳng c,d,m,n,p cắt nhau đôi một ,trong đó có ba đường thẳng m,n,p cùng đi qua một điểm . Hãy cho biết có tất cả bao nhiêu giao điểm?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
23 tháng 11 2015
số đường thẳng tạo bởi n điểm ( không có 3 điểm nào thẳng hàng ) là : n(n-1):2
ta có : n(n-1):2 =55 => n(n-1) = 110 = 11. (11-1) => n =11
Vậy có 11 điêrm
ST
23 tháng 11 2015
Ta có : \(\frac{n\left(n-1\right)}{2}=55\)( đường thẳng )
\(\Rightarrow n\left(n-1\right)=55.2\)( đường thẳng )
\(n\left(n-1\right)=110\)( đường thẳng )
\(\Rightarrow n=11\)
XO
7 tháng 1 2019
Số điểm còn lại là 40 - 10 = 30
Ta có : Lấy một điểm bất kì ta vẽ được 29 đường thẳng
=> trong 30 điểm đó ta vẽ được (30 . 29) : 2 = 435 đường thẳng
10 điểm còn lại vì qua hai điểm mới vẽ được 1 đường thẳng
=> lấy 1 điểm bất kì vẽ được 10 - 1 = 9 đường thẳng
=> 10 điểm còn lại vẽ được 10 . 9 : 2 = 45 đường thẳng
=> 40 điểm đó ta vẽ được 45 + 435 = 480 đường thẳng
CM
20 tháng 10 2019
Câu đúng: a) và g).
Câu sai: b), c), d), e), f), h).
Giải thích:
- Câu b sai vì nếu ba điểm( phân biệt) cho trước là ba điểm thẳng hàng thì có đúng 1 đường thẳng đi qua ba điểm đó.
- Câu c sai vì nếu bốn điểm ( phân biệt) cho trước là bốn điểm thẳng hàng thì có đúng 1 đường thẳng đi qua bốn điểm đó.
- Câu d sai vì hai đường thẳng phân biệt có thể song song hoặc cắt nhau.
- Câu e sai vì hai đường thẳng không cắt nhau có thể trùng nhau hoặc song song.
- Câu f sai vì hai đường thẳng không song song có thể có thể trùng nhau hoặc cắt nhau.
- Câu h sai vì ba đường thẳng phân biệt, đôi một cắt nhau thì có thể có đúng 1 giao điểm. Như hình vẽ dưới đây.
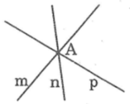
Có 8 giao điểm