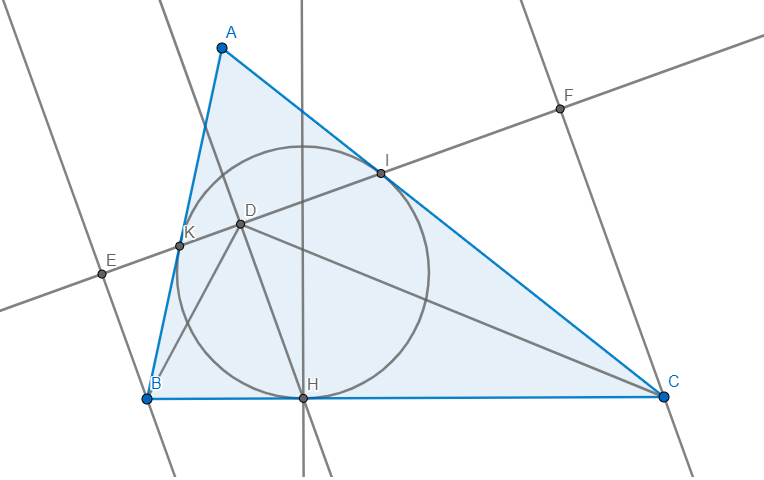
cho tam giác abc. Đường tròn nội tiếp tam giác tiếp xúc các cạnh BC, CA, AB tại D, E, F. Hạ DH vuông góc DE. CMR: HD là tia phân giác góc BHC
Giúp mình vs
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AT
19 tháng 7 2021
Kẻ \(BE\bot IK,CF\bot IK\)
Vì AK,AI là tiếp tuyến \(\Rightarrow\Delta AKI\) cân tại A \(\Rightarrow\angle AKI=\angle AIK\)
\(\Rightarrow\angle BKE=\angle CIF\)
Xét \(\Delta BEK\) và \(\Delta CFI:\) Ta có: \(\left\{{}\begin{matrix}\angle BKE=\angle CIF\\\angle BEK=\angle CFI=90\end{matrix}\right.\)
\(\Rightarrow\Delta BEK\sim\Delta CFI\left(g-g\right)\Rightarrow\dfrac{BE}{CF}=\dfrac{BK}{CI}\)
Vì BK,BH là tiếp tuyến \(\Rightarrow BH=BK\)
Vì CI,CH là tiếp tuyến \(\Rightarrow CI=CH\)
\(\Rightarrow\dfrac{BK}{CI}=\dfrac{BH}{CH}\Rightarrow\dfrac{BE}{CF}=\dfrac{BH}{CH}\)
Vì \(BE\parallel HD\parallel CF(\bot IK)\) \(\Rightarrow\dfrac{BH}{CH}=\dfrac{ED}{DF}\Rightarrow\dfrac{BE}{CF}=\dfrac{ED}{DF}\)
Xét \(\Delta BED\) và \(\Delta CFD:\) Ta có: \(\left\{{}\begin{matrix}\dfrac{BE}{CF}=\dfrac{DE}{DF}\\\angle BED=\angle CFD=90\end{matrix}\right.\)
\(\Rightarrow\Delta BED\sim\Delta CFD\left(c-g-c\right)\Rightarrow\angle BDE=\angle CDF\)
mà \(\angle AKI=\angle AIK\Rightarrow\angle AKI-\angle BDE=\angle AIK-\angle CDF\)
\(\Rightarrow\angle ABD=\angle ACD\)
