Mn giúp em câu 5 với
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


-Gọi số vịt trong trại chăn nuôi là a (con)
- Vì số gà bằng \(\dfrac{2}{5}\) số vịt
=> số gà là: a:\(\dfrac{2}{5}\)=\(\dfrac{5}{2}\)a (con)
=> tổng số gà và vịt là: a+\(\dfrac{5}{2}\)a=266
=> a=76
=> số gà là: 190 (con)
Vậy có 190 con gà và 76 con vịt trong trại chăn nuôi
Tóm tắt:
1 trại:266con và vịt
Số gà:\(\dfrac{2}{5}\)số vịt
trại đó :...con gà?
trại đó:...con vịt
bài giải
Ta có sơ đồ:
Con gà:xx xin lỗi mk chỉ thế thôi
con vịt:xxxxx và tổng 266 con
theo sơ đồ,tổng số phần bằng nhau là:
2+5=7(phần)
Trại đó nuôi số con gà là:
266\(\div\)7\(\times\)2=76(con)
Trại đó nuôi số con vịt là:
266-76=190(con)
Đ/S:Gà:76 con.
Vịt:190 con.
Chúc bạn học tốt.



Câu 5:
TL:Phải biết giúp đỡ nhưng người có hoàn cảnh khó khăn,....

Bài 4:
a) Thay x=49 vào B ta có:
\(B=\dfrac{1-\sqrt{49}}{1+\sqrt{49}}=-\dfrac{3}{4}\)
b) \(A=\left(\dfrac{15-\sqrt{x}}{x-25}+\dfrac{2}{\sqrt{x}+5}\right):\dfrac{\sqrt{x}+1}{\sqrt{x}-5}\)
\(A=\left[\dfrac{15-\sqrt{x}}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-5\right)}+\dfrac{2\left(\sqrt{x}-5\right)}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-5\right)}\right]\cdot\dfrac{\sqrt{x}-5}{\sqrt{x}+1}\)
\(A=\dfrac{15-\sqrt{x}+2\sqrt{x}-10}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-5\right)}\cdot\dfrac{\sqrt{x}-5}{\sqrt{x}+1}\)
\(A=\dfrac{\sqrt{x}+5}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-5\right)}\cdot\dfrac{\sqrt{x}-5}{\sqrt{x}+1}\)
\(A=\dfrac{1}{\sqrt{x}-5}\cdot\dfrac{\sqrt{x}-5}{\sqrt{x}+1}\)
\(A=\dfrac{1}{\sqrt{x}+1}\)
c) Ta có:
\(M=A-B=\dfrac{1}{\sqrt{x}+1}-\dfrac{1-\sqrt{x}}{\sqrt{x}+1}\)
\(M=\dfrac{1-1+\sqrt{x}}{\sqrt{x}+1}\)
\(M=\dfrac{\sqrt{x}}{\sqrt{x}+1}\)
\(M=\dfrac{\sqrt{x}+1-1}{\sqrt{x}+1}=\dfrac{\sqrt{x}+1}{\sqrt{x}+1}-\dfrac{1}{\sqrt{x}+1}=1-\dfrac{1}{\sqrt{x}+1}\)
Mà M nguyên khi:
\(1\) ⋮ \(\sqrt{x}+1\)
\(\Rightarrow\sqrt{x}+1\in\left\{1;-1\right\}\)
Mà: \(\sqrt{x}+1\ge1\)
\(\Rightarrow\sqrt{x}+1=1\)
\(\Rightarrow\sqrt{x}=0\)
\(\Rightarrow x=0\left(tm\right)\)
Vậy M nguyên khi x=0


 Mn giúp em câu 5 với
Mn giúp em câu 5 với





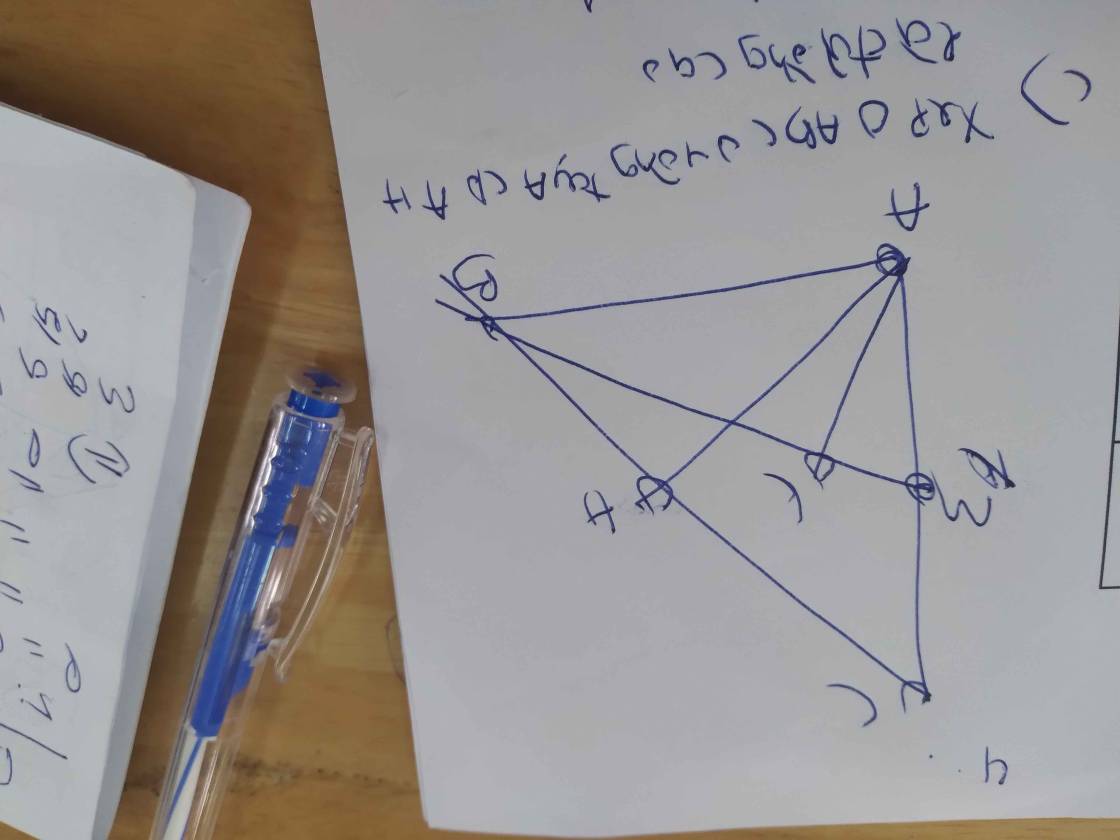


 mn giúp e câu C của bài 4 và 5 với ạ,em cảm ơn
mn giúp e câu C của bài 4 và 5 với ạ,em cảm ơn
a)
$n_{CuO} = \dfrac{4}{80} = 0,05(mol)$
$CuO + 2HCl \to CuCl_2 + H_2O$
Theo PTHH : $n_{HCl} = 2n_{CuO} = 0,05.2 = 0,1(mol)$
$C_{M_{HCl}} = \dfrac{0,1}{0,04} = 2,5M$
b)
$n_{CuCl_2} = n_{CuO} = 0,05(mol)$
$m_{CuCl_2} = 0,05.135 = 6,75(gam)$