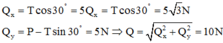Một thanh AB cứng đồng chất, tiết diện đều, có khối lượng riêng là D =1,5\(\dfrac{g}{cm^3}\), có chiều dài L = 21cm. Đặt thanh tì lên mép 1 chậu chứa nước rộng và không đầy, sao cho đầu B trong chậu bắt đầu nổi thì thanh ngập 1/3 chiều dài trong nước. Hãy xác định khoảng cách từ điểm tì O đến đầu A của thanh.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a/ Gọi K là điểm giao nhau giữa mực nc và thah AB, G là trung điểm của thanh mà trọng lực của thanh sẽ tập trung tại đây
gọi H là TĐ của KB
Vậy thì ta cần tìm KB
Có OA= OB/2\(\Rightarrow OA=\frac{l}{3}=\frac{40}{3}\left(cm\right)\Rightarrow OB=\frac{2l}{3}=\frac{80}{3}\left(cm\right)\)
có \(AG=BG=\frac{AB}{2}=20\left(cm\right)\)
Có \(OG+AO=AG\Rightarrow OG=AG-AO=20-\frac{1}{2}OB=20-\frac{1}{2}.\frac{80}{3}=\frac{20}{3}\left(cm\right)\)
Có H là TĐ của KB\(\Rightarrow KH=HB=\frac{KB}{2}\)
\(\Rightarrow OH=OK+KH=OB-KB+\frac{1}{2}KB=\frac{80}{3}-\frac{1}{2}KB\)
Trọng lượng của thanh là:
\(P=d_t.V_{AB}=11200.S.l_{AB}=448000S\left(N\right)\)
Lực đẩy ASM t/d lên thanh là:
\(F_A=d_n.V_{KB}=10000.S.l_{KB}\left(N\right)\)
Theo PTĐB:
P.OG= FA.OH
\(\Leftrightarrow448000S.\frac{20}{3}=10000S.l_{KB}.\left(\frac{80}{3}-\frac{1}{2}l_{KB}\right)\)
Giải ra tìm lKB là xong
Câu b làm tương tự để tìm D của chất lỏng

1.Rải
*Cái \(\Delta\)mà bạn nói ko quan trong lắm đâu, nó để gọi các ẩn chưa biết để tìm ra ẩn đó thôi. VD như \(\Delta t\),\(\Delta m\),... giống bạn gọi x trong toán đó. Còn cái \(\Delta\)trong toán có nghĩa khác bạm tự tìm hiểu nhe!(Theo ý nghĩ của mình)![]()
*LB:
Thể tích phần nước dâng lên là:\(V_n=\Delta h.\left(2S-S\right)=0,04.S\)
Do phần nước dâng lên chính bằng thể tích phần chìm của vật.
<=>Ta có: \(Fa=P\)
<=>\(V_n.D_n.10=V.D.10\)
<=>\(\Delta h.S.D_n=h.S.D\)
<=>\(\Delta h.D_n=h.D\)<=>\(h=\dfrac{D_n.\Delta h}{D}=\dfrac{1000.0,04}{800}=0,05\left(m\right)\)
Vậy h thanh trụ là: h = 0,05(m) = 5(cm).


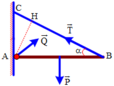
Thanh AB là một đòn bẩy có điểm tựa tại O. Các lực tác dụng lên đòn bẩy AB:
- Trọng lực của thah AB đặt tại trung điểm G của thanh AB, chiều từ trên xuống, cánh tay đòn là đoạn GH.
- Lực đẩy Ác-si-mét nước tác dụng lên thanh AB, có điểm đặt tại trung điểm N của đoạn GB bị ngập trong nước, chiều từ dưới lên, cánh tay đòn là đoạn KN.
Thanh Ab đang cân bằng nên theo điều kiện cân bằng của đòn bẩy ta có:
\(P.GH=F_A.NK\left(1\right)\)
Gọi trọng lượng riêng của thanh là D, trọng lượng riêng của nước là Dn, S là tiêt diện đáy của thanh, l là chiều dài thanh.
Ta có:
\(P=10D.S.l\\ F_A=10D_n.S.\dfrac{l}{2}\)
Thay vào (1) ta được:
\(10D.S.l.GH=10D_n.S.\dfrac{l}{2}.NK\\ \Rightarrow D.GH=D_n.\dfrac{1}{2}NK\\ \Rightarrow D=\dfrac{NK.D_n}{2GH}\left(2\right)\)
Xét \(\Delta OHG\) và \(\Delta OKN\) có:
\(\widehat{OHG}=\widehat{OKN}=90^o\)
\(\widehat{N}\): góc chung
\(\Rightarrow\Delta OHG\approx\Delta OKN\left(g-g\right)\)
Do đó:
\(\dfrac{NK}{GH}=\dfrac{ON}{OM}\)
Ta có:
\(ON=OB-NB=\dfrac{2l}{3}-\dfrac{l}{4}=\dfrac{5l}{12}\\ OG=AG-AO=\dfrac{l}{2}-\dfrac{l}{3}=\dfrac{l}{6}\)
\(\Rightarrow\dfrac{NK}{GH}=\dfrac{ON}{OM}=\dfrac{\dfrac{5l}{12}}{\dfrac{l}{6}}=\dfrac{5}{2}\)
Thay vào (2) ta được:
\(D=\dfrac{5.D_n}{2.2}=\dfrac{5.1000}{4}=1250\)(kg/m3)
Vậy khối lượng riêng của thanh kim loại là 1250kg/m3.

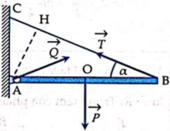
- Thanh chịu tác dụng của trọng lực P đặt tại trung điểm M của thanh AB và lực đẩy Acsimet tại trung điểm N của đoạn MB. Thanh có thể quay quanh O. Áp dụng quy tắc cân bằng đòn bẩy ta có:
P . MH = F . NK (1)
- Gọi S là tiết diện, l là chiều dài của thanh. Ta có:
P = 10. S. D. l và F = 10. Dn.S.\(\frac{1}{2}\)
- Thay vào (1) . Ta có: D=\(\frac{NK}{2MH}.D_n\)
- Mặt khác △OHM∼△OKN Ta có:
\(\frac{KN}{MH}=\frac{ON}{OM}\) Trong đó: ON = OB - MB =\(\frac{l}{3}-\frac{l}{4}=\frac{5l}{12}\)
OM= AM - OA = \(\frac{l}{2}-\frac{l}{3}=\frac{l}{6}\)
\(\frac{KN}{MH}=\frac{ON}{OM}=\frac{5}{2}\) .Thay vào 2 ta được \(D=\frac{5}{4}.D_n=1250kg\)/m3
Vậy khối lượng riêng của thanh đó là 1250