Giải giúp em câu b với, câu b thôi nha. Em cảm ơn nhiều ạ! 
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


c) A = x.M + (4x + 7)/(√x + 3)
= 3x/(√x + 3) + (4x + 7)/(√x + 3)
= (7x + 7)/(√x + 3)
Để A nhỏ nhất thì 7x + 7 nhỏ nhất
Mà x ≥ 0
⇒ 7x + 7 ≥ 7
⇒ GTNN của A là 7/3 khi x = 0

\(A=\sqrt{2a\left(b+1\right)}+\sqrt{2b\left(c+1\right)}+\sqrt{2c\left(a+1\right)}\)
\(A=\dfrac{1}{\sqrt{2}}\sqrt{4a\left(b+1\right)}+\dfrac{1}{\sqrt{2}}\sqrt{4b\left(c+1\right)}+\dfrac{1}{\sqrt{2}}\sqrt{4c\left(a+1\right)}\)
\(A\le\dfrac{1}{2\sqrt{2}}\left(4a+b+1\right)+\dfrac{1}{2\sqrt{2}}\left(4b+c+1\right)+\dfrac{1}{2\sqrt{2}}\left(4c+a+1\right)\)
\(A\le\dfrac{1}{2\sqrt{2}}\left[5\left(a+b+c\right)+3\right]=2\sqrt{2}\)
\(A_{max}=2\sqrt{2}\) khi \(a=b=c=\dfrac{1}{3}\)

10.
\(H\left(x\right)=-5x^4+10x^3-15x+1\)
\(=-5x\left(x^3-2x^2+3\right)+1\)
\(=-5x.0+1\)
\(=1\)
9.
\(P\left(x\right)-Q\left(x\right)=\left(1-a\right)x^3+x^2+x-6\)
\(P\left(x\right)-Q\left(x\right)\) là đa thức bậc 3 khi và chỉ khi \(1-a\ne0\)
\(\Rightarrow a\ne1\)

1: (x-1)^2+(y+2)^2=25
=>R=5; I(1;-2)
2: Δ'//Δ nên Δ': 3x-4y+c=0
d(I;Δ')=5
=>\(\dfrac{ \left|3\cdot1+\left(-2\right)\cdot\left(-4\right)+c\right|}{\sqrt{3^2+\left(-4\right)^2}}=5\)
=>|c+11|=25
=>c=14 hoặc c=-36
=>3x-4y+14=0 hoặc 3x-4y-36=0
3x-4y+14=0
=>VTPT là (3;-4) và (Δ') đi qua A(2;5)
=>VTCP là (4;3)
=>PTTS là x=2+4t và y=5+3t
3x-4y-36=0
=>VTPT là (3;-4) và (Δ') đi qua B(0;-9)
=>VTCP là (4;3)
PTTS là x=0+4t và y=-9+3t


1: vecto AC=(-2;2)
=>VTCP là (-2;2); vtpt là (2;2)
2: vecto AB=(-10;-2)=(5;1)
=>VTPT của Δ là (5;1)
vtcp của Δ là (-1;5)
\(\overrightarrow{AC}=\left(-2;2\right)=2\left(-1;1\right)\) nên đường thẳng AC nhận \(\left(-1;1\right)\) là 1 vtcp và \(\left(1;1\right)\) là 1 vtpt
b.
\(\overrightarrow{BA}=\left(10;2\right)=2\left(5;1\right)\) ; mà \(\Delta\perp AB\) nên \(\Delta\) nhận (5;1) là 1 vtpt và \(\left(1;-5\right)\) là 1 vtcp

thay \(x=3-2\sqrt{2}\) vào P ta có:
\(\dfrac{x+8}{\sqrt{x}+1}=\dfrac{3-2\sqrt{2}+8}{\sqrt{3-2\sqrt{2}}+1}=\dfrac{11-2\sqrt{2}}{\sqrt{2}-1+1}=\dfrac{11-2\sqrt{2}}{\sqrt{2}}\)
\(b,x=3-2\sqrt{2}=\left(\sqrt{2}-1\right)^2\)
Thay vào P, ta được:
\(P=\dfrac{3-2\sqrt{2}+8}{\sqrt{\left(\sqrt{2}-1\right)^2}+1}=\dfrac{11-2\sqrt{2}}{\sqrt{2}}=\dfrac{11\sqrt{2}-4}{2}\)

bạn chỉ cần tách x4-1 thành (x2-1)(x2+1),rồi đặt x2=t là ok







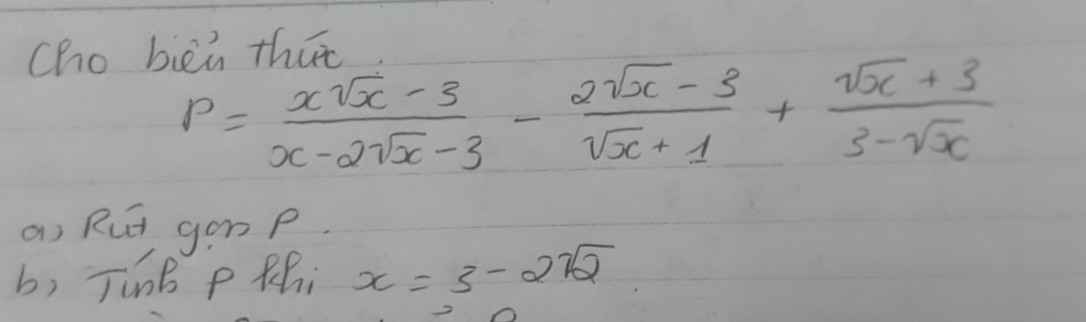
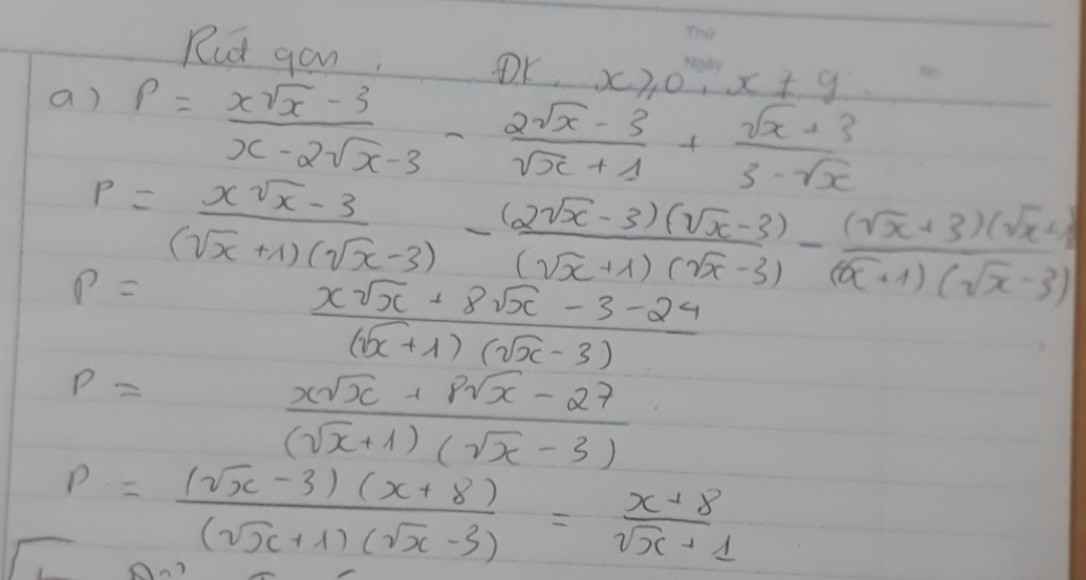


Phương trình đường thẳng d' qua M và vuông góc \(\Delta\) (nên nhận \(\left(1;1\right)\) là 1 vtpt) có dạng:
\(1\left(x-3\right)+1\left(y-2\right)=0\Leftrightarrow x+y-5=0\)
Gọi H là giao điểm d' và \(\Delta\Rightarrow\) tọa độ H là nghiệm:
\(\left\{{}\begin{matrix}x-y=0\\x+y-5=0\end{matrix}\right.\) \(\Rightarrow H\left(\dfrac{5}{2};\dfrac{5}{2}\right)\)
M' là ảnh của M qua phép đối xứng trục \(\Rightarrow\) H là trung điểm MM'
\(\Rightarrow\left\{{}\begin{matrix}x_{M'}=2x_H-x_M=2\\y_{M'}=2y_H-y_M=3\end{matrix}\right.\) \(\Rightarrow M'\left(2;3\right)\)
Gọi \(d_1\) là ảnh của d qua phép đối xứng trục
Gọi A là giao điểm d và \(\Delta\Rightarrow A\in d_1\), tọa độ A thỏa mãn:
\(\left\{{}\begin{matrix}x+4y-3=0\\x-y=0\end{matrix}\right.\) \(\Rightarrow A\left(\dfrac{3}{5};\dfrac{3}{5}\right)\)
Lấy \(B\left(3;0\right)\) là 1 điểm thuộc d
Phương trình đường thẳng \(\Delta'\) qua B và vuông góc \(\Delta\) có dạng:
\(1\left(x-3\right)+1\left(y-0\right)=0\Leftrightarrow x+y-3=0\)
Gọi C là giao điểm \(\Delta\) và \(\Delta'\Rightarrow\) tọa độ C thỏa mãn:
\(\left\{{}\begin{matrix}x+y-3=0\\x-y=0\end{matrix}\right.\) \(\Rightarrow C\left(\dfrac{3}{2};\dfrac{3}{2}\right)\)
B' là ảnh của B qua phép đối xứng trục \(\Delta\Rightarrow B'\in d_1\) và C là trung điểm BB'
\(\Rightarrow\left\{{}\begin{matrix}x_{B'}=2x_C-x_B=0\\y_{B'}=2y_C-y_B=3\end{matrix}\right.\) \(\Rightarrow B'\left(0;3\right)\)
\(\Rightarrow\overrightarrow{AB'}=\left(-\dfrac{3}{5};\dfrac{12}{5}\right)=\dfrac{3}{5}\left(-1;4\right)\)
\(\Rightarrow d_1\) nhận (4;1) là 1 vtpt
Phương trình \(d_1\):
\(4\left(x-0\right)+1\left(y-3\right)=0\Leftrightarrow4x+y-3=0\)
THật sự cảm ơn anh rất rất nhiều