Tam giác ABC cân ở A. 3 đường cao AD BE CF. Đường thẳng AC cắt đường thẳng qua B và song song với CF tại H.
a, cm AH.AE=AC^2
b, 1/CF^2=1/BC^2+1/4AD^2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AT
28 tháng 7 2021
Vì tam giác ABC cân tại A có đường cao AH nên D là trung điểm BC
Từ C kẻ đường thẳng vuông góc với BC cắt AB tại G
\(\Rightarrow CG\parallel AD\) mà D là trung điểm BC \(\Rightarrow A\) là trung điểm BG
nên AD là đường trung bình tam giác BCG \(\Rightarrow AD=\dfrac{CG}{2}\)
\(\Rightarrow2AD=CG\Rightarrow4AD^2=CG^2\)
tam giác BCG vuông tại C có đường cao CF nên áp dụng hệ thức lượng
\(\Rightarrow\dfrac{1}{BC^2}+\dfrac{1}{CG^2}=\dfrac{1}{CF^2}\Rightarrow\dfrac{1}{BC^2}+\dfrac{1}{4AD^2}=\dfrac{1}{CF^2}\)
CH
Cô Hoàng Huyền
Admin
VIP
12 tháng 7 2017
Cô hướng dẫn nhé.
a) Do ABC là tam giác cân nên AE = AF, AC = AB
Lại có \(\Delta AFC\sim\Delta ABH\left(g-g\right)\Rightarrow\frac{AF}{AB}=\frac{AC}{AH}\Rightarrow AF.AH=AB.AC\Rightarrow AE.AH=AC^2\)
b) Câu này đề ko đúng. Cô sửa lại \(\frac{1}{CF^2}=\frac{1}{BC^2}+\frac{1}{4.AD^2}\)
\(AD.BC=AB.CF\left(=\frac{S_{ABC}}{2}\right)\)
Vậy nên \(VP=\frac{AD^2+\frac{BC^2}{4}}{BC^2.AD^2}=\frac{AD^2+\left(\frac{BC}{2}\right)^2}{CF^2AB^2}=\frac{AD^2+BD^2}{CF^2AB^2}=\frac{AB^2}{CF^2.AB^2}=\frac{1}{CF^2}=VT\)
CM
5 tháng 11 2017
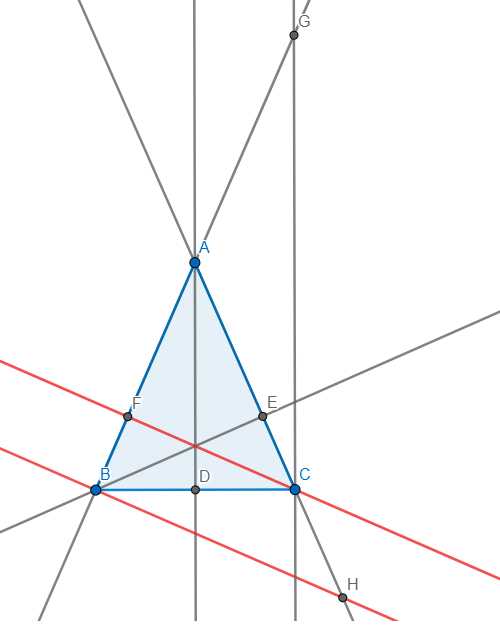
Gọi diện tích các hình tam giác ABC, MAB, MAC, MBC lần lượt là S, S 1 , S 2 , S 3 . Ta có:
S = S 1 + S 2 + S 3
Trong đó: S = 1/2 AD.BC = 1/2 BE. AC = 1/2 CF. AB
S 1 = 1/2 MT. AB
S 2 = 1/2 MK. AC
S 3 = 1/2 MH. BC
Y
23 tháng 6 2019
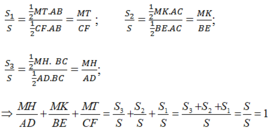
18. a) Dễ cm : AE = AF
+ EF // BH \(\Rightarrow\frac{AF}{AB}=\frac{AC}{AH}\Rightarrow\frac{AE}{AC}=\frac{AC}{AH}\)
\(\Rightarrow AC^2=AE\cdot AH\Rightarrow AC=\sqrt{AE\cdot AH}\)
b) Qua C kẻ đg thẳng // với AD cắt AB tại I
+ AD là đg TB của ΔBCI
=> CI = 2AD \(\Rightarrow CI^2=\left(2AD\right)^2=4AD^2\)
+ CI // AD => CI ⊥ BC
+ ΔBCI vuông tại C, đg cao CF
\(\Rightarrow\frac{1}{CF^2}=\frac{1}{BC^2}+\frac{1}{CI^2}=\frac{1}{BC^2}+\frac{1}{4AD^2}\)
bài cuối tương tự câu a) bài trên
Y
23 tháng 6 2019
16. Qua B kẻ đg thẳng // với AC cắt CD tại I
Gọi BH là chiều cao của hình thang ABCD
+ BI // AC => BI ⊥ BD
+ Tứ giác ABIC là hbh => AB = CI
=> AB + CD = CD + CI = DI
+ ΔBDH vuông tại H
\(\Rightarrow DH=\sqrt{BD^2-BH^2}=20\) ( cm )
+ ΔBDI vuông tại B, đg cao BH
\(\Rightarrow BD^2=DH\cdot DI\)
\(\Rightarrow DI=\frac{29^2}{20}=42,05\) ( cm )
=> Độ dài đg TB của hình thang ABCD là :
\(\frac{1}{2}\left(AB+CD\right)=\frac{1}{2}DI=21,025\) ( cm )
a, Ta có: \(BH//CF\left(gt\right)\)
\(CF\perp AB\left(gt\right)\)
\(\Rightarrow BH\perp AB\)
\(\Delta ABH\)có: \(\widehat{ABH}=90^o,BH\perp AB\)
\(\Rightarrow AB^2=AE.AH\)(hệ thức lượng trong tam giác vuông)
\(AB=AC\left(gt\right)\)
\(\Rightarrow AC^2=AH.AE\)
Câu b chiều mình làm nhé
b, Kẻ \(DG\perp AB\)
Ta có: \(DG\perp AB\left(cd\right)\)
\(FC\perp AB\left(gt\right)\)
\(\Rightarrow DG//FC\)
\(\Delta ABC\)cân tại A có: AD là đường cao của \(\Delta ABC\)\(\Rightarrow\)AD là đường trung tuyến của \(\Delta ABC\)\(\Rightarrow BD=DC\)
\(\Delta BEC\)có: \(DG//FC\left(cmt\right)\)
\(BD=DC\left(cmt\right)\)
\(\Rightarrow GF=FB\)
\(\Delta BFC\)có: \(GF=FB\left(cmt\right)\)
\(BD=DC\left(cmt\right)\)
\(\Rightarrow\)\(\hept{\begin{cases}DG//FC\\DG=\frac{1}{2}FC\end{cases}}\)
\(\Delta ADB\)có: \(\widehat{ADB}=90^o,DG\perp AB\)
\(\Rightarrow\frac{1}{DG^2}=\frac{1}{AD^2}+\frac{1}{DB^2}\)(hệ thức về cạnh và đường cao trong tam giác vuông)
mà \(DG=\frac{1}{2}FC\left(cmt\right)\)
\(\Rightarrow\frac{4}{FC^2}=\frac{1}{AD^2}+\frac{1}{DB^2}\)
mà \(BD=\frac{1}{2}BC\left(cmt\right)\)
\(\Rightarrow\frac{4}{FC^2}=\frac{1}{AD^2}+\frac{4}{BC^2}\)\(\Leftrightarrow\frac{1}{FC^2}=\frac{1}{4AD^2}+\frac{1}{BC^2}\)