Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cô hướng dẫn nhé.
a) Do ABC là tam giác cân nên AE = AF, AC = AB
Lại có \(\Delta AFC\sim\Delta ABH\left(g-g\right)\Rightarrow\frac{AF}{AB}=\frac{AC}{AH}\Rightarrow AF.AH=AB.AC\Rightarrow AE.AH=AC^2\)
b) Câu này đề ko đúng. Cô sửa lại \(\frac{1}{CF^2}=\frac{1}{BC^2}+\frac{1}{4.AD^2}\)
\(AD.BC=AB.CF\left(=\frac{S_{ABC}}{2}\right)\)
Vậy nên \(VP=\frac{AD^2+\frac{BC^2}{4}}{BC^2.AD^2}=\frac{AD^2+\left(\frac{BC}{2}\right)^2}{CF^2AB^2}=\frac{AD^2+BD^2}{CF^2AB^2}=\frac{AB^2}{CF^2.AB^2}=\frac{1}{CF^2}=VT\)

Vì tam giác ABC cân tại A có đường cao AH nên D là trung điểm BC
Từ C kẻ đường thẳng vuông góc với BC cắt AB tại G
\(\Rightarrow CG\parallel AD\) mà D là trung điểm BC \(\Rightarrow A\) là trung điểm BG
nên AD là đường trung bình tam giác BCG \(\Rightarrow AD=\dfrac{CG}{2}\)
\(\Rightarrow2AD=CG\Rightarrow4AD^2=CG^2\)
tam giác BCG vuông tại C có đường cao CF nên áp dụng hệ thức lượng
\(\Rightarrow\dfrac{1}{BC^2}+\dfrac{1}{CG^2}=\dfrac{1}{CF^2}\Rightarrow\dfrac{1}{BC^2}+\dfrac{1}{4AD^2}=\dfrac{1}{CF^2}\)

a, Ta có: \(BH//CF\left(gt\right)\)
\(CF\perp AB\left(gt\right)\)
\(\Rightarrow BH\perp AB\)
\(\Delta ABH\)có: \(\widehat{ABH}=90^o,BH\perp AB\)
\(\Rightarrow AB^2=AE.AH\)(hệ thức lượng trong tam giác vuông)
\(AB=AC\left(gt\right)\)
\(\Rightarrow AC^2=AH.AE\)
Câu b chiều mình làm nhé
b, Kẻ \(DG\perp AB\)
Ta có: \(DG\perp AB\left(cd\right)\)
\(FC\perp AB\left(gt\right)\)
\(\Rightarrow DG//FC\)
\(\Delta ABC\)cân tại A có: AD là đường cao của \(\Delta ABC\)\(\Rightarrow\)AD là đường trung tuyến của \(\Delta ABC\)\(\Rightarrow BD=DC\)
\(\Delta BEC\)có: \(DG//FC\left(cmt\right)\)
\(BD=DC\left(cmt\right)\)
\(\Rightarrow GF=FB\)
\(\Delta BFC\)có: \(GF=FB\left(cmt\right)\)
\(BD=DC\left(cmt\right)\)
\(\Rightarrow\)\(\hept{\begin{cases}DG//FC\\DG=\frac{1}{2}FC\end{cases}}\)
\(\Delta ADB\)có: \(\widehat{ADB}=90^o,DG\perp AB\)
\(\Rightarrow\frac{1}{DG^2}=\frac{1}{AD^2}+\frac{1}{DB^2}\)(hệ thức về cạnh và đường cao trong tam giác vuông)
mà \(DG=\frac{1}{2}FC\left(cmt\right)\)
\(\Rightarrow\frac{4}{FC^2}=\frac{1}{AD^2}+\frac{1}{DB^2}\)
mà \(BD=\frac{1}{2}BC\left(cmt\right)\)
\(\Rightarrow\frac{4}{FC^2}=\frac{1}{AD^2}+\frac{4}{BC^2}\)\(\Leftrightarrow\frac{1}{FC^2}=\frac{1}{4AD^2}+\frac{1}{BC^2}\)

\({}\)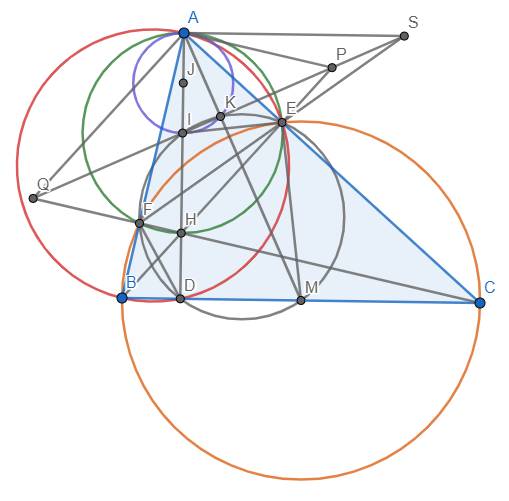
a) Vì \(\widehat{BEC}=\widehat{BFC}=90^o\) nên tứ giác BEFC nội tiếp đường tròn đường kính BC. Tương tự như thế, tứ giác AEDB nội tiếp đường tròn đường kính AB. Cũng có \(\widehat{AEH}=\widehat{AFH}=90^o\) nên tứ giác AEHF nội tiếp đường tròn đường kính AH.
Ta có \(\widehat{IEM}=\widehat{IEB}+\widehat{BEM}\)
\(=\left(90^o-\widehat{IEA}\right)+\widehat{EBC}\)
\(=90^o-\widehat{EAD}+\widehat{EBD}=90^o\) (do \(\widehat{EBD}=\widehat{EAD}\))
Vậy \(IE\perp ME\)
b) Dễ thấy các điểm I, D, E, F, M, K cùng thuộc đường tròn đường kính IM. Gọi J là trung điểm AI thì I chính là tâm của đường tròn (AIK) nên (J) tiếp xúc với (I) tại A. Dẫn đến A nằm trên trục đẳng phương của (I) và (J)
Mặt khác, ta có \(SK.SI=SE.SF\) nên \(P_{S/\left(I\right)}=P_{S/\left(J\right)}\) hay S nằm trên trục đẳng phương của (I) và (J). Suy ra AS là trục đẳng phương của (I) và (J). \(\Rightarrow\)\(AS\perp IJ\) hay AS//BC (đpcm).
c) Ta thấy tứ giác AKEP nội tiếp đường tròn AP
\(\Rightarrow\widehat{APB}=\widehat{MKE}=\widehat{MDE}=\widehat{BAC}\)
\(\Rightarrow\Delta BAE~\Delta BPA\left(g.g\right)\Rightarrow\widehat{BAP}=\widehat{BEA}=90^o\)
\(\Rightarrow\) AP//QH \(\left(\perp AB\right)\)
\(\Rightarrow\widehat{IAP}=\widehat{IHQ}\) (2 góc so le trong)
Từ đó dễ dàng chứng minh \(\Delta IAP=\Delta IHQ\left(g.c.g\right)\) \(\Rightarrow IP=IQ\) hay I là trung điểm PQ (đpcm)