Một tam giác vuông cân có cạnh góc vuông bằng 7 cm . Độ dài cạnh huyền bằng ? cm .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Vì một cạnh góc vuông = 5cm => cạnh góc vuông kia cũng = 5cm
Theo định lý PTG ta có: 5^2 + 5^2 = cạnh huyền^2
25 + 25 = 50
=> cạnh huyền = \(\sqrt{50}\)(cm)
Tam giác vuông cân
=> Hai cạnh góc vuông bằng nhau
Và cùng bằng 5 cm
Độ dài cạnh huyền là: \(\sqrt{5^2+5^2}=5\sqrt{2}\) (cm) (Áp dụng định lý Pytago trong tam giác vuông)

Tam giác vuông cân là tam giác vuông có 2 cạnh góc vuông bằng nhau. Gọi độ dài cạnh góc vuông là x (cm) (x > 0)
Áp dụng định lí pitago ta có:
x2 +x2 =(√2)2⇒ 2x2 = 2 => x2 =1
=> x=1cm

Đáp án A
Gọi độ dài cạnh góc vuông nhỏ hơn của tam giác vuông đó là x (cm); (0 < x < 20)
Cạnh góc vuông lớn hơn của tam giác vuông có độ dài là: x + 4
Vì cạnh huyền bằng 20 cm nên theo định lý Py-ta-go ta có:
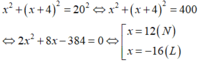
Vậy độ dài hai cạnh góc vuông của tam giác vuông đó lần lượt là: 12 cm và 12 + 4 = 16 cm

Đáp án A
Gọi độ dài cạnh góc vuông nhỏ hơn của tam giác vuông đó là x (cm); (0 < x < 20)
Cạnh góc vuông lớn hơn của tam giác vuông có độ dài là: x + 4
Vì cạnh huyền bằng 20 cm nên theo định lý Py-ta-go ta có:
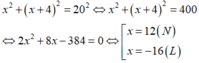
Vậy độ dài hai cạnh góc vuông của tam giác vuông đó lần lượt là: 12 cm và 12 + 4 = 16 cm

Vì tam giác trên là tam giác vuông cân
=> Cạnh đáy bằng cạnh góc vuông
Áp dụng định lí Py - ta - go ta có :
Cạnh huyền2 = cạnh góc vuông2 + cạnh đáy2 = 22 +22 = 8
=> Cạnh huyền = \(\sqrt{8}\)(cm)

Đặt cạnh huyền của tam giác là x (\(x > 8\))
Theo giải thiết ta tính được cạnh góc vuông là \(x - 8\)
Áp dụng định lý Pitago ta tính được cạnh góc vuông còn lại là \(\sqrt {{x^2} - {{\left( {x - 8} \right)}^2}} = \sqrt {16x - 64} \)
Ta có chu vi của tam giác là \(x + \left( {x - 8} \right) + \sqrt {16x - 64} = 30\)
\(\begin{array}{l} \Leftrightarrow \sqrt {16x - 64} = 38 - 2x\\ \Rightarrow 16x - 64 = {\left( {38 - 2x} \right)^2}\\ \Rightarrow 16x - 64 = 1444 - 152x + 4{x^2}\\ \Rightarrow 4{x^2} - 168x + 1508 = 0\end{array}\)
\( \Rightarrow x = 13\) và \(x = 29\)
Thay \(x = 13\) và \(x = 29\) vào phương trình \(\sqrt {16x - 64} = 38 - 2x\) ta thấy chỉ có \(x = 13\) thảo mãn phương trình
Vậy cạnh huyền có độ dài là 13 cm.

4:
a: Gọi độ dài cạnh góc vuông cần tìm là x
Theo đề, ta có: x^2+x^2=a^2
=>2x^2=a^2
=>x^2=a^2/2=2a^2/4
=>\(x=\dfrac{a\sqrt{2}}{2}\)
b:
Độ dài cạnh là;
\(h:\dfrac{\sqrt{3}}{2}=\dfrac{2h}{\sqrt{3}}\)
5:
ΔAHB vuông tại H
=>AH^2+HB^2=AB^2
=>13^2=12^2+HB^2
=>HB=5cm
BC=5+16=21cm
ΔAHC vuông tại H
=>AH^2+HC^2=AC^2
=>AC^2=16^2+12^2=400
=>AC=20(cm)

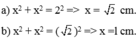
Gọi tam giác đó vuông cân tại A, 2 góc ở đáy là B và C
Áp dụng định lý Pytago ta có :
BC^2 = AB^2 + AC^2
hay BC^2 = 7^2 + 7^2 = 98
=> BC = \(\sqrt{98}\)
Vậy,...........