Tìm giá trị lớn nhất, nhỏ nhất của phương trình sau :
y=4*sin(x+2𝜋/3)+1
y=cos2x +5sinx + 2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 9 2021
1. Không dịch được đề
2.
\(-1\le cos2x\le1\Rightarrow1\le y\le3\)
3.
a. \(-2\le2sinx\le2\Rightarrow-1\le y\le3\)
\(y_{min}=-1\) khi \(sinx=-1\Rightarrow x=-\dfrac{\pi}{2}+k2\pi\)
\(y_{max}=3\) khi \(sinx=1\Rightarrow x=\dfrac{\pi}{2}+k2\pi\)
b.
\(0\le cos^2x\le1\Rightarrow-1\le y\le2\)
\(y_{min}=-1\) khi \(cos^2x=1\Rightarrow x=k\pi\)
\(y_{max}=2\) khi \(cosx=0\Rightarrow x=\dfrac{\pi}{2}+k\pi\)
4.
\(y=\left(tanx-1\right)^2+2\ge2\)
\(y_{min}=2\) khi \(tanx=1\Rightarrow x=\dfrac{\pi}{4}+k\pi\)
21 tháng 8 2023
a: -1<=sinx<=1
=>5>=-5sinx>=-5
=>11>=-5sinx+6>=1
=>1<=y<=11
\(y_{min}=1\) khi sin x=1
=>x=pi/2+k2pi
\(y_{max}=11\) khi sin x=-1
=>x=-pi/2+k2pi
b: \(-1< =cosx< =1\)
=>\(1>=-cosx>=-1\)
=>\(-3>=-cosx-4>=-5\)
=>\(-3>=y>=-5\)
\(y_{min}=-5\) khi cosx=1
=>x=k2pi
\(y_{max}=-3\) khi cosx=-1
=>x=pi+k2pi
c: \(-1< =cosx< =1\)
=>\(-\sqrt{3}< \sqrt{3}\cdot cosx< =\sqrt{3}\)
=>\(-\sqrt{3}+8< =y< =\sqrt{3}+8\)
\(y_{min}=-\sqrt{3}+8\) khi cosx=-1
=>x=pi+k2pi
\(y_{max}=\sqrt{3}+8\) khi cosx=1
=>x=k2pi
d: \(-1< =cos3x< =1\)
=>\(1>=-cos3x>=-1\)
=>\(16>=y>=14\)
y min=14 khi cos3x=1
=>3x=k2pi
=>x=k2pi/3
y max=16 khi cos3x=-1
=>3x=pi+k2pi
=>x=pi/3+k2pi/3
e: -1<=sin6x<=1
=>-1+2024<=sin6x+2024<=1+2024
=>2023<=y<=2025
y min=2023 khi sin6x=-1
=>6x=-pi/2+k2pi
=>x=-pi/12+kpi/3
y max=2025 khi sin6x=1
=>6x=pi/2+k2pi
=>x=pi/12+kpi/3
CM
9 tháng 9 2019
Chọn B
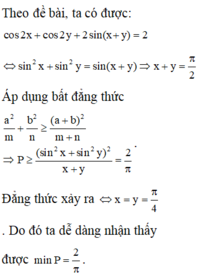
Bổ trợ kiến thức: Ở đây để giải quyết bài toán các em cần có 2 bước trung gian rất quan trọng, thứ nhất là với
x
,
y
∈
0
;
π
2
thì 
và một bất đẳng thức các em đã được học ở lớp dưới là: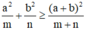 
.
Nếu như xử lí trực tiếp bài toán trên mà không phải qua các bước trung gian thì rất là khó, điều quan trọng là các em phải biết áp dụng các bước trung gian sao cho hợp lí để đưa bài toán đến kết quả nhanh nhất có thể.