Cho đoạc thẳng DC.Trên tia đối của tia DC lấy A,trên tia đối của tia CD lấy B sao cho AC \(\ge\)BD.
CMR:BC\(\le\)AD
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

vì a nằm trên đoạn thẳng cd nên a thuộc đường thẳng cd
vì b nằm trên đoạn thẳng cd nên b thuộc đường thẳng cd
suy ra; ac bằng bd

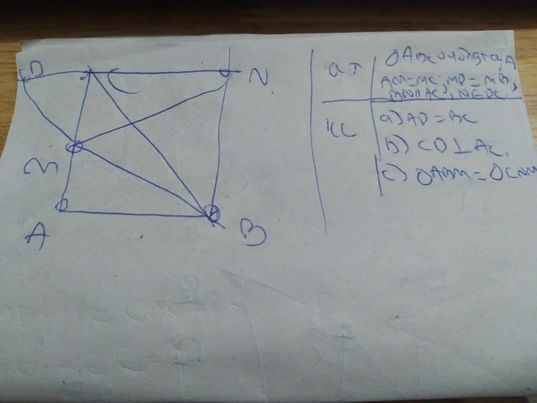
a: Xét ΔAMD và ΔCMB có
MA=MC
\(\widehat{AMD}=\widehat{CMB}\)
MD=MB
Do đó: ΔAMD=ΔCMB
=>AD=BC
b: Xét ΔMAB và ΔMCD có
MA=MC
\(\widehat{AMB}=\widehat{CMD}\)
MB=MD
Do đó: ΔMAB=ΔMCD
=>\(\widehat{MAB}=\widehat{MCD}=90^0\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//CD
=>CD\(\perp\)AC
c: Xét tứ giác ABNC có
AB//NC
AC//BN
Do đó: ABNC là hình bình hành
=>CN=AB
Xét ΔMAB vuông tại A và ΔMCN vuông tại C có
MA=MC
AB=CN
Do đó: ΔMAB=ΔMCN
Vì AC\(\ge\)BD nên AC+CD\(\ge\)BD+CD
hay AD\(\ge\)BC (vì các điểm A,B,C,D cùng nằm trên 1 đường thẳng)