Cho tứ giác ABCD. Chứng minh AC + BD < AC + BC +CD + AD.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
22 tháng 7 2018
P/s : Chứng minh rằng AC + BD < AB + BC + CD + DA .
Gọi O là giao điểm của hai đường chéo AC và BD .
Ta có :
Xét tam giác OAB có :
\(OA+OB>AB\) ( bất đẳng thức trong tam giác ) (1)
Xét tam giác OBC có :
\(OB+OC>BC\)( BĐT tam giác ) (2)
Xét tam giác ODC có :
\(OD+OC>DC\) (BĐT tam giác )(3)
Xét tam giác OAD có :
\(OA+OD>AD\) (4)
Cộng từng vế ta có :
\(AC+BD< AB+BC+CD+DA\) (đpcm)
KC
0
TP
0
19 tháng 7 2016
A B C D O
Gọi O là giao điểm hai đường chéo AC và BD
- Xét lần lượt các tam giác OAB , OBC , OCD , OAD và áp dụng bất đẳng thức tam giác được :
\(OA+OB>AB\) ; \(OB+OC>BC\) ; \(OC+OD>CD\) ; \(OA+OD>AD\)
Cộng các bất đẳng thức trên theo vế được : \(2\left(OA+OB+OC+OD\right)>AB+BC+CD+AD\)
\(\Rightarrow2\left(AC+BD\right)>AB+BC+CD+AD\) \(\Rightarrow AC+BD>\frac{AB+BC+CD+DA}{2}\) (1)
- Tương tự, lần lượt xét các tam giác ACD , BCD , BAC , ABD và áp dụng bất đẳng thức tam giác được :
\(AD+CD>AC\) ; \(BC+CD>BD\) ; \(AB+BC>AC\) ; \(AB+AD>BD\)
Cộng các bất đẳng thức trên theo vế được : \(2\left(AC+BD\right)< 2\left(AB+BC+CD+DA\right)\)
\(\Rightarrow AC+BD< AB+BC+CD+DA\)(2)
Từ (1) và (2) ta có : \(\frac{AB+BC+CD+DA}{2}< AC+BD< AB+BC+CD+AD\)
hay \(\frac{AB+BC+CD+DA}{2}< OA+OB+OC+OD< AB+BC+CD+AD\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
19 tháng 7 2023
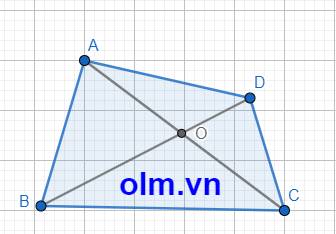
Xét \(\Delta\)AOD ta có: AO + OD > AD (trong 1 tam giác tổng hai cạnh luôn lớn hơn cạnh còn lại)
Xét \(\Delta\) OCD ta có: BO + OC > BC ( trong 1 tam giác tổng hai cạnh luôn lớn hơn cạnh còn lại)
Cộng vế với vế ta có: AO + OD + BO + OC > AD + BC
(AO + OC) + ( OD + OB > AD + BC
AC+ BD > AD + BC
Chứng Minh tương tự ta có: AC + BD > AB + CD
1 tháng 9 2017
Câu này dễ mà.Mình học lớp 7 mà mình còn biết nữa đó.Chắc bạn thắc mắc là vì sao mình học lớp 7 mà mình biết bài lớp 8 đúng không.Tại vì mình có thi học sinh giỏi và đạt giải nhì vòng trường lớp 6 luôn đấy,thấy mình giỏi không.
TA
1
ND
15 tháng 6 2019
Gọi O là giao điểm 2 đường chéo của tứ giác ABCD.
Xét :Tam giác BOC có: BC < OB + OC (bất đẳng thức trong tam giác)
Tam giác AOD có: AD < OD + OA (.............................................)
Do đó: BC + AD < (OB + OD) +(OC + OA)
hay BC + AD < BD + AC
Mà AD = AC (GT) => BC < BD.
A B C D O