Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) Ta có \(\Delta ABC\)cân tại A \(\Rightarrow\widehat{ABC}=\frac{180^o-\widehat{BAC}}{2}\left(1\right)\)
Do BD là phân giác \(\widehat{ABC}\)\(\Rightarrow\widehat{ABD}=\widehat{DBC}\)
CE là phân giác \(\widehat{ACB}\)\(\Rightarrow\widehat{ACE}=\widehat{ECB}\)
Mà \(\Delta ABC\)cân \(\Rightarrow\widehat{ABC}=\widehat{ACB}\)
Suy ra \(\widehat{ABD}=\widehat{DBC}=\widehat{ACE}=\widehat{ECB}\)
Xét \(\Delta ABD=\Delta ACE\left(g-c-g\right)\)( tự xét nha :)))
\(\Rightarrow AD=AE\)\(\Rightarrow\Delta AED\)cân tại A
\(\Rightarrow\widehat{AED}=\frac{180^o-\widehat{BAC}}{2}\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\widehat{AED}=\widehat{ABC}\)
Mà hai góc đó ở vị trí đồng vị
\(\Rightarrow ED//BC\)
Lại có : \(\widehat{ABC}=\widehat{ACB}\)
Suy ra : BEDC là hình thang cân (3)
Ta có : \(ED//BC\Rightarrow\widehat{EDB}=\widehat{DBC}\)( so le trong )
Mà \(\widehat{EBD}=\widehat{DBC}\)
Suy ra \(\widehat{EDB}=\widehat{EBD}\)\(\Rightarrow\Delta BED\)cân tại E
\(\Rightarrow EB=ED\left(4\right)\)
Từ (3) và (4) \(\Rightarrow\)BEDC là hình thang cân có cạnh bên bằng đáy nhỏ -_-
b) Xét \(\Delta ABH=\Delta ACK\left(ch-gn\right)\)( tự xét )
\(\Rightarrow AK=AH\)\(\Rightarrow\Delta AKH\)cân tại A
\(\Rightarrow\widehat{AKH}=\frac{180^o-\widehat{BAC}}{2}\left(5\right)\)
Từ (1) và (5) \(\Rightarrow\widehat{AKH}=\widehat{ABC}\)
Mà hai góc trên ở vị trí đồng vị
Suy ra : KH // BC
Lại có : \(\widehat{ABC}=\widehat{ACB}\)
Suy ra : BKHC là hình thang cân
c) Do BM là trung tuyến \(\Rightarrow AM=\frac{1}{2}AC\)
CN là trung tuyến \(\Rightarrow AN=\frac{1}{2}AB\)
Mà AB = AC \(\Rightarrow AN=AM\)
\(\Rightarrow\Delta AMN\)cân tại A \(\Rightarrow\widehat{ANM}=\frac{180^o-\widehat{BAC}}{2}\left(6\right)\)
Từ (1) và (6) \(\Rightarrow\widehat{ANM}=\widehat{ABC}\)
Mà hai góc trên ở vị trí đồng vị
\(\Rightarrow MN//BC\)
Lại có : \(\widehat{ABC}=\widehat{ACB}\)
Suy ra BNMC là hình thang cân
Vậy ...
CHO TAM GIÁC ABC CÂN TẠI A
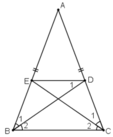
A/ĐƯỜNG PHÂN GIÁC BD,EC (D ∈ AC ,E ∈ AB).CMR TỨ GIÁC BEDC LÀ HÌNH THANG CÂN CÓ CẠNH BÊN BẰNG ĐÁY NHỎ
B/ĐƯỜNG CAO BH,CK (H ∈ AC, K ∈ AB).CMR: BKHC LÀ HÌNH THANG CÂN
C/ĐƯỜNG TRUNG TUYẾN BM ,CN (M ∈ AC, N ∈ AB). CMR :BNCM LÀ HÌNH THANG CÂN
GIÚP VS BẠN ƠI
a: Xét ΔADB và ΔAEC có
góc BAD chung
AB=AC
góc ABD=góc ACE
Do đó: ΔADB=ΔAEC
Xét ΔABC có AE/AB=AD/AC
nên ED//BC
=>BEDC là hình thang
mà góc EBC=góc DCB
nên BEDC là hình thang cân
Xét ΔEDB có góc EDB=góc EBD(=góc DBC)
nên ΔEDB cân tại E
=>BE=ED=DC
b: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
góc BAH chung
Do đó ΔAHB=ΔAKC
=>AH=AK
Xét ΔABC có AK/AB=AH/AC
nên KH//BC
=>BKHC là hình thang
mà góc KBC=góc HCB
nên BKHC là hình thang cân
c: Xét ΔABC có AN/AB=AM/AC
nên NM//BC
=>BNMC là hình thang
mà góc B=góc C
nên BNMC là hình thang cân
a: Xét ΔADB và ΔAEC có
góc BAD chung
AB=AC
góc ABD=góc ACE
Do đó: ΔADB=ΔAEC
b: Xét ΔABC có AE/AB=AD/AC
nên ED//BC
=>BEDC là hình thang
mà góc EBC=góc DCB
nên BEDC là hình thang cân
Xét ΔEDB có góc EDB=góc EBD(=góc DBC)
nên ΔEDB cân tại E
=>BE=ED=DC
- Chứng minh tứ giác BCDE là hình thang cân:
+ ΔABC cân tại A 
BD là phân giác của 
CE là phân giác của 
+ Xét ΔAEC và ΔADB có:
⇒ ΔAEC = ΔADB
⇒ AE = AD
Vậy tam giác ABC cân tại A có AE = AD
Theo kết quả bài 15a) suy ra BCDE là hình thang cân.
- Chứng minh ED = EB.
ED // BC ⇒ 
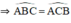
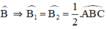
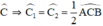
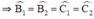
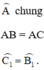
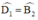(Hai góc so le trong)
Mà 
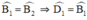⇒ ΔEDB cân tại E ⇒ ED = EB.
Vậy ta có EBCD là hình thang cân có đáy nhỏ bằng cạnh bên.
Ta có : tam giác ABC cân tại A
BD là phân giác của góc ABC
CE là phân giác của góc ACB
=>BD=CE (trong tam giác cân 2 đường phân giác xuất phát từ 2 góc đáy của tam giác bằng nhau . p/s: nếu bạn k bik định lí này bạn có thể chứng minh nhé)
Xét tam giác ABD và tam giác ACE :
BD=CE (cmt)
góc ABD= góc ACE (góc ABC=góc ACB=2 góc ABD= 2 góc ACE)
AB=BC (tam giác ABC cân tại A)
Suy ra: tam giác ABD= tam giác ACE (c-g-c)
=>AD=AE ( 2 cạnh tương ứng)
=>tam giác ADE cân tại A
Mà tam giác ABC cũng cân tại A nên:
góc ABC = góc ACB= góc ADE= goác ADE
Ta lại có: góc ABC và góc AED ở vị trí đồng vị nên:
ED//BC
=>BEDC là hình thang
Mà BD=CE
nên: BEDC là hình thang cân(1)
Ta có: ED//BC => góc DEC = góc ECB
Mà góc ECB= góc DCE ( CE là p/g của góc ACE)
=> góc DEC=góc DCE
=> tam giác DEC cân tại D
=>ED=DC (2)
Từ (1) và (2) suy ra: BEDC là hình thang cân có đáy nhò bằng cạnh bên.
Bài b ko biết hi hi k mình ra
Tiếp câu b .
Có : \(\Delta ABC\) cân tại A
=> \(\widehat{ABC}=\widehat{ACB}\) (1)
Theo tổng 3 góc trong 1 tam giác :
Với \(\Delta ABC\) => \(\widehat{ABC}+\widehat{ACB}+\widehat{A}=180^0\)
=> \(\widehat{ABC}+\widehat{ACB}=130^0\)
Lại có (1)
=> \(\widehat{ABC}=\widehat{ACB}=\frac{130^0}{2}=65^0\)
Vì tứ giác là hình thang cân (chắc cũng biết tứ giác nào nhỉ :v )
=> ED // BC
=> \(\widehat{DEB}+\widehat{EBC}=180^0\)
=> \(\widehat{DEB}=180^0-65^0=115^0\)
Tương tự với góc \(\widehat{EDC}\)
Ta có : tam giác ABC cân tại A
BD là phân giác của góc ABC
CE là phân giác của góc ACB
=>BD=CE (trong tam giác cân 2 đường phân giác xuất phát từ 2 góc đáy của tam giác bằng nhau . p/s: nếu bạn k bik định lí này bạn có thể chứng minh nhé)
Xét tam giác ABD và tam giác ACE :
BD=CE (cmt)
góc ABD= góc ACE (góc ABC=góc ACB=2 góc ABD= 2 góc ACE)
AB=BC (tam giác ABC cân tại A)
Suy ra: tam giác ABD= tam giác ACE (c-g-c)
=>AD=AE ( 2 cạnh tương ứng)
=>tam giác ADE cân tại A
Mà tam giác ABC cũng cân tại A nên:
góc ABC = góc ACB= góc ADE= goác ADE
Ta lại có: góc ABC và góc AED ở vị trí đồng vị nên:
ED//BC
=>BEDC là hình thang
Mà BD=CE
nên: BEDC là hình thang cân(1)
Ta có: ED//BC => góc DEC = góc ECB
Mà góc ECB= góc DCE ( CE là p/g của góc ACE)
=> góc DEC=góc DCE
=> tam giác DEC cân tại D
=>ED=DC (2)
Từ (1) và (2) suy ra: BEDC là hình thang cân có đáy nhò bằng cạnh bên.
Hok tốt ! Nếu thấy đúng thì k cho mìn !
a: Xét ΔADB và ΔAEC có
góc ABD=góc ACE
AB=AC
góc A chung
Do đó: ΔADB=ΔAEC
Suy ra: AD=AE
Xét ΔABC có AE/AB=AD/AC
nên ED//BC
=>BEDC là hình thang
mà CE=BD
nên BEDC là hình thag cân
Xét ΔEDB có góc EDB=góc EBD
nên ΔEDB cân tại E
=>BE=ED=DC
b: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
góc A chung
Do đó: ΔAHB=ΔAKC
Suy ra: AH=AK
Xét ΔABC có AK/AB=AH/AC
nên KH//BC
=>BKHC là hình thang
mà CK=BH
nên BKHC là hình thang cân
c: Xét ΔABC có
N là trung điểm của AB
M là trung điểm của AC
Do đó: NM là đường trung bình
=>NM//BC
hay BNMC là hình thang
mà góc B=góc C
nên BNMC là hình thang cân