cho góc xoy điểm a nằm trong góc đo qua ox và oy vẽ điểm d và e ll đối xứng với điểm a gọi b và c theo thứ tự là giao điểm của đề với ox và oy cm tam giác abc có chu vi nn trong các tam giác có đỉnh là a và hai dionh còn lại thuộc ox và xy
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
20 tháng 4 2016
)Tam giác ABC có AB=30cm, AC=40cm. Trên tia đối của tia AC lấy điểm D sao cho AD=AB. Qua A kẻ đường d vuông góc với BD. Gọi M là điểm bất kì thuộc đường thẳng d. Tìm giá trị nhỏ nhất của tổng BM+MC
7 tháng 10 2021
a: Ta có: AE+EB=AB
AF+FC=AC
mà AB=AC
và EB=FC
nên AE=AF
hay A nằm trên đường trung trực của FE(1)
Xét ΔEBH và ΔFCH có
EB=FC
\(\widehat{B}=\widehat{C}\)
BH=CH
Do đó: ΔEBH=ΔFCH
Suy ra: HE=HF
hay H nằm trên đường trung trực của FE(2)
Từ (1) và (2) suy ra E và F đối xứng nhau qua AH
CM
5 tháng 6 2019
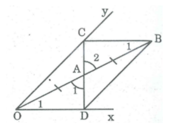
Xét ∆ OAD và ∆ BAC, ta có:
OA = AB (tính chất đối xứng tâm)
∠ A 1 = ∠ A 2 (đối đỉnh)
∠ O 1 = ∠ B 1 (so le trong)
Do đó: ∆ OAD = ∆ BAC (g.c.g)
⇒ AD = AC
Suy ra: C đối xứng với D qua A.