Ai giúp em được k ạ e cảm ơn
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.





\(26,\\ a,\sin45^0=\cos45^0< \sin50^025'< \sin57^048'=\cos32^012'< \sin72^0=\cos18^0< \sin75^0\\ b,\tan37^026'< \tan47^0< \tan58^0=\cot32^0< \tan63^0< \tan66^019'=\cot23^041'\\ 27,\\ A=\dfrac{\left(\sin^226^0+\sin^264^0\right)+2\left(\cos^215^0+\cos^275^0\right)}{\left(\sin^255^0+\cos^255^0\right)+\left(\sin^242^0+\cos^242^0\right)}-\dfrac{\tan81^0}{2\tan81^0}\\ A=\dfrac{\left(\sin^226^0+\cos^226^0\right)+2\left(\sin^215^0+\cos^215^0\right)}{1+1}-\dfrac{1}{2}\\ A=\dfrac{1+2}{2}-\dfrac{1}{2}=2-\dfrac{1}{2}=\dfrac{3}{2}\)
\(28,\\ \sin^2\alpha=1-\cos^2\alpha=1-\dfrac{1}{2}=\dfrac{1}{2}\\ \Leftrightarrow\sin\alpha=\dfrac{\sqrt{2}}{2}\)

\(\dfrac{x-13}{87}-1+\dfrac{x-27}{73}-1+\dfrac{x-67}{33}-1+\dfrac{x-73}{27}-1=0\)
\(\Leftrightarrow\dfrac{x-100}{87}+\dfrac{x-100}{73}+\dfrac{x-100}{33}+\dfrac{x-100}{27}=0\)
\(\Leftrightarrow\left(x-100\right)\left(\dfrac{1}{87}+\dfrac{1}{73}+\dfrac{1}{33}+\dfrac{1}{27}\ne0\right)=0\Leftrightarrow x=100\)


Ta có \(\dfrac{1}{2^2}< \dfrac{1}{1.2};\dfrac{1}{3^2}< \dfrac{1}{2.3};...;\dfrac{1}{2022^2}< \dfrac{1}{2021.2022}\)
cộng vế với vế
\(\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{2022^2}< 1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{2021}-\dfrac{1}{2022}\)
\(=1-\dfrac{1}{2022}=\dfrac{2021}{2022}\)
Vậy ta có đpcm

\(\dfrac{x+4}{3}=\dfrac{x-11}{-6}\)
\(\dfrac{2x+8}{6}=\dfrac{-x+11}{6}\)
\(\Leftrightarrow2x+8=-x+11\)
\(\Leftrightarrow3x=3\)
\(\Leftrightarrow x=1\)

6) \(\left(2x+\dfrac{1}{2}\right)^3=8x^3+4x^2+\dfrac{3}{2}x+\dfrac{1}{8}\)
7) \(\left(x-3\right)^3=x^3-9x^2+27x-27\)





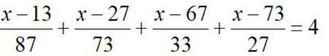
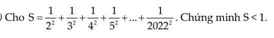
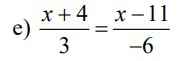
 ai giúp em với ạ :3 e cảm ơn m.ng trước !! thân ái
ai giúp em với ạ :3 e cảm ơn m.ng trước !! thân ái
\(a,\left(x-3\right)^2+\left(x+3\right)^2-\left(x-2\right)\left(x+2\right)\)
\(=x^2-6x+9+x^2+6x+9-x^2+4=x^2+22\)
\(b,x^2+22=|3|^2+22=9+22=31\)
\(c,x^2+22\)
Vì \(x^2\ge0\) \(\Rightarrow\) \(x^2+22\ge22\left(\forall x\right)\)
Dấu ''='' xảy ra \(\Leftrightarrow\) \(x^2=0\)
\(\Leftrightarrow\) \(x=0\)
vậy giá trị nhỏ nhất của A là:
Min A = 22 khi x = 0