Cho đường tròn (O) và điểm B nằm trên đường tròn. Kẻ tiếp tuyến của (O) tại B, trên đó lấy điểm A. trên OA lấy điểm C sao cho AB = AC, tia BC cắt (O) tai E. Chứng minh rằng OE vuông góc với OA.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CH
Cô Hoàng Huyền
Admin
VIP
25 tháng 11 2016
Vì tam giác ABC cân tại A nên \(\widehat{ACB}=\widehat{ABC}\)
Lại có \(\widehat{ACB}\) và \(\widehat{OCE}\) là hai góc đối đỉnh nên chúng bằng nhau. Nói cách khác \(\widehat{OCE}=\widehat{ABC}\)
Do OE = OB nên \(\widehat{OEB}=\widehat{OBE}\)
Mà \(\widehat{ABC}+\widehat{OBE}=90^o\Rightarrow\widehat{OCE}+\widehat{OEB}=90^o\Rightarrow\widehat{EOC}=90^o.\)
Vậy \(OE\perp OA.\)
10 tháng 1 2023
a: ΔOBC cân tại O
mà OH là đường cao
nên H là trung điểm của BC nên OH là phân giác của góc BOC
OH*OA=OB^2=R^2
b: Xét ΔOBA và ΔOCA có
OB=OC
góc BOA=góc COA
OA chung
Do đo: ΔOBA=ΔOCA
=>góc OCA=90 độ
=>AC là tiếp tuyến của (O)
1 tháng 10 2021
a: Gọi H là trung điểm của OA
Xét (O) có
OH là một phần đường kính
BC là dây
OH⊥BC tại H
Do đó: H là trung điểm của BC
Xét tứ giác ABOC có
H là trung điểm của đường chéo AO
H là trung điểm của đường chéo BC
Do đó: ABOC là hình bình hành
mà OB=OC
nên ABOC là hình thoi
CM
12 tháng 4 2018
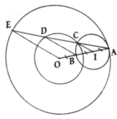
a, Gọi I là trung điểm của AB, ta có: OI = OA – IA
b, Ta chứng minh được IC//BD//OE
Mà OB = BI = IA => AC = CD = DE