Question

[Tríp Bô Hắc]

Câu 1: Cho tam giác ABC vuông tại A . Trên cạnh BC lấy điểm D, kẻ DN
vuông góc với AC và DM vuông góc AB . Kẻ đường cao AH của tam giác ABC .
a. Tứ giác AMDN là hình gì ? Vì sao?
b. Tìm vị trí điểm D trên cạnh BC thì MN có độ dài nhỏ nhất ? vẽ hình đúng
với vị trí của điểm D đó?
c. Tính số đo góc MHN ?
Câu 2:
a) Tìm các giá trị x ; y nguyên dương sao cho 9xy +3x +3y =51
b) Tìm giá trị nhỏ nhất của đa thức N = x2 + 5y2 - 4xy + 6x - 14y + 15

Answer 1

[Trần Quốc Lộc]

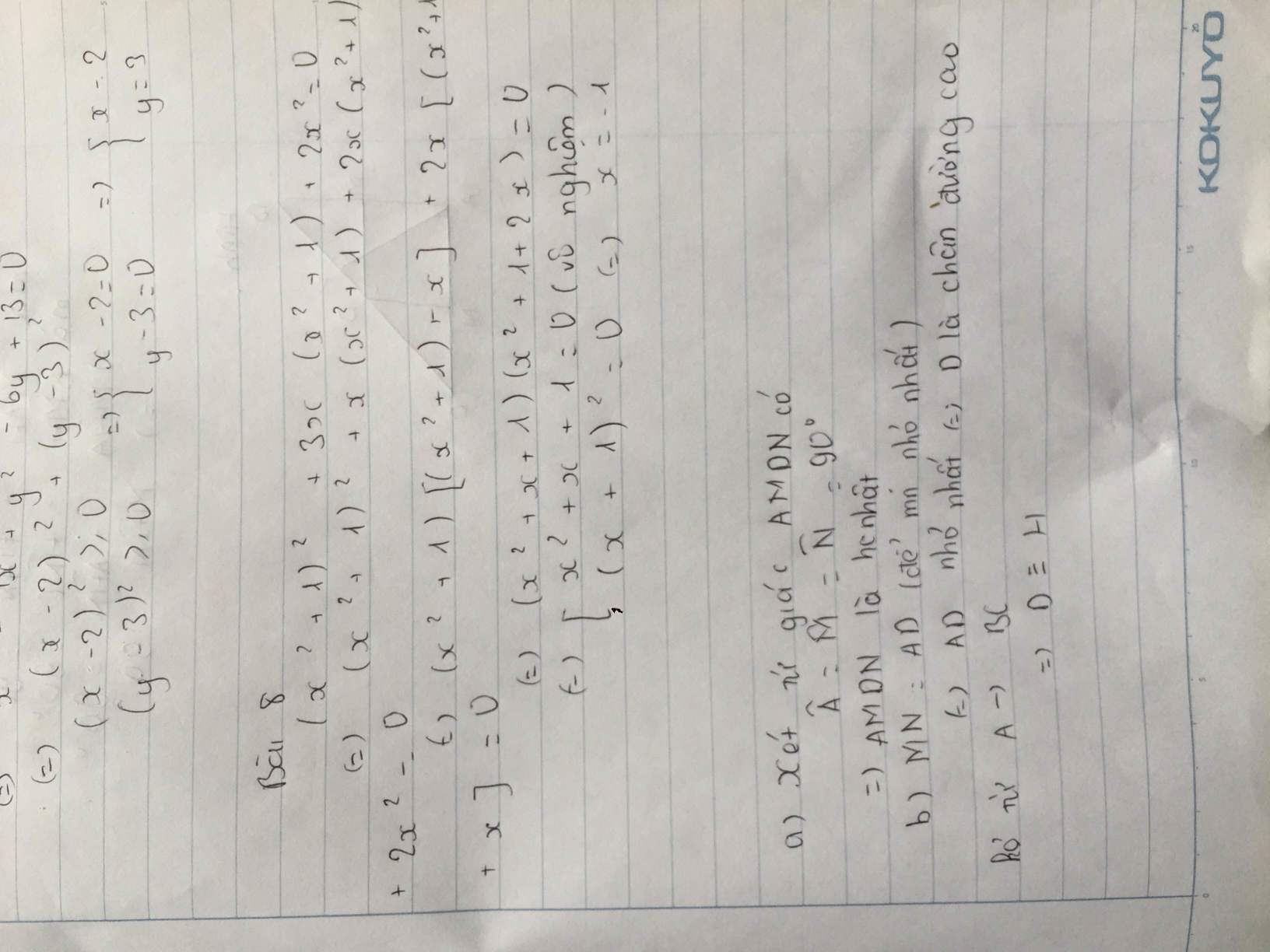
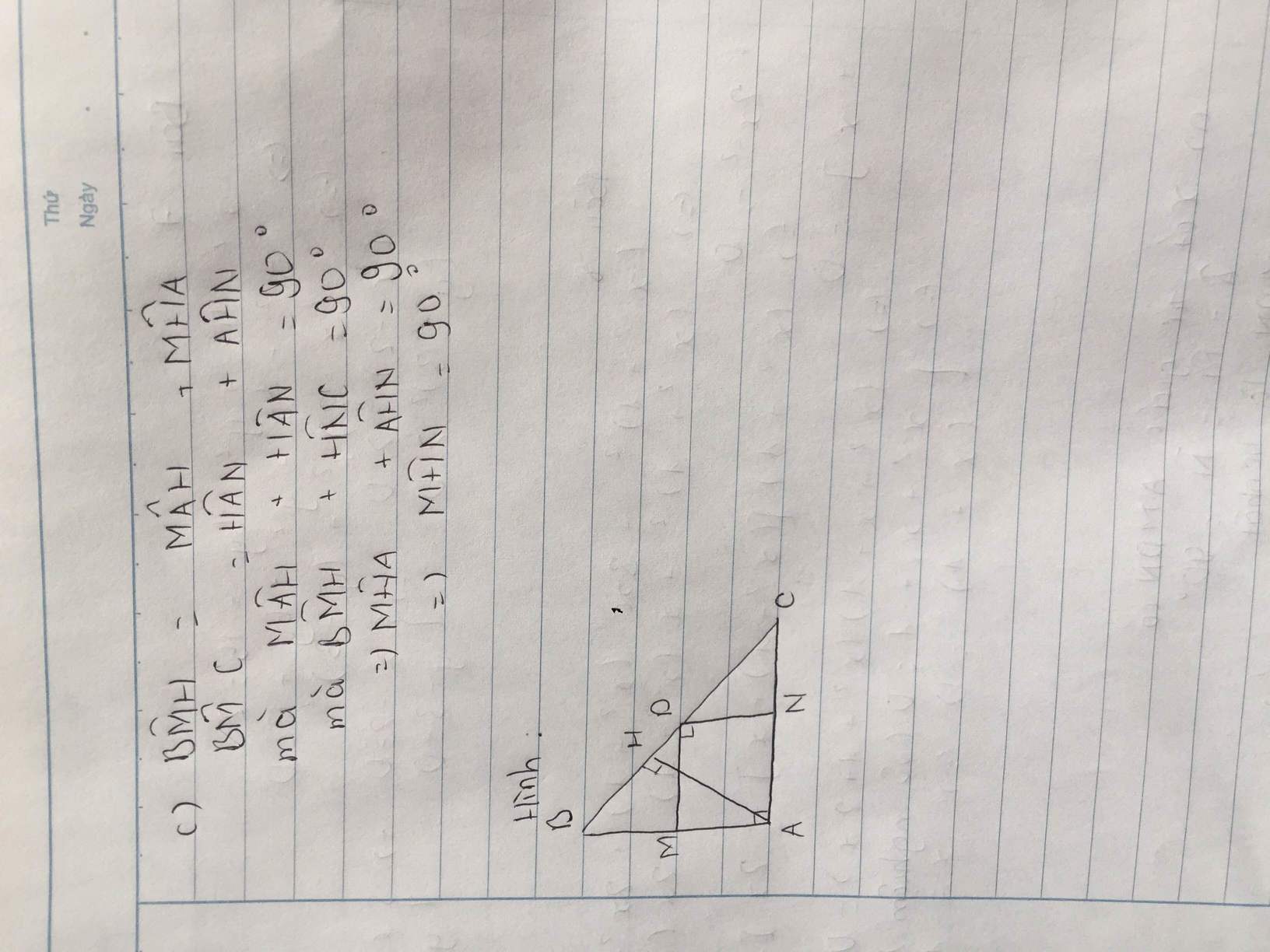
Câu 2:

\(9xy+3x+3y=51\\ \Leftrightarrow\left(9xy+3x\right)+\left(3y+1\right)=52\\ \Leftrightarrow3x\left(3y+1\right)+\left(3y+1\right)=52\\ \Leftrightarrow\left(3x+1\right)\left(3y+1\right)=52\)

Lập bảng giá trị :

\(3x+1\)	\(1\)	\(2\)	\(4\)	\(13\)	\(26\)	\(52\)
\(x\)	\(0\left(loại\right)\)	\(\dfrac{1}{3}\left(loại\right)\)	\(1\)	\(4\)	\(\dfrac{25}{3}\left(loại\right)\)	\(17\)
\(3y+1\)	\(52\)	\(26\)	\(13\)	\(4\)	\(2\)	\(1\)
\(y\)	\(17\)	\(\dfrac{25}{3}\left(loại\right)\)	\(4\)	\(1\)	\(\dfrac{1}{3}\left(loại\right)\)	\(0\left(loại\right)\)

Vậy cặp số nguyên dương \(\left\{x;y\right\}=\left\{4;1\right\};\left\{1;4\right\}\)

\(\text{ b) }N=x^2+5y^2-4xy+6x-14y+15\\ =\left(x^2+4y^2+9-4xy+6x-12y\right)+\left(y^2-2y+1\right)+5\\ =\left(x-2y+3\right)^2+\left(y-1\right)^2+5\)

Do \(\left(y-1\right)^2\ge0\forall x\)

\(\left(x-2y+3\right)^2\ge0\forall x\\ \Rightarrow\left(x-2y+3\right)^2+\left(y-1\right)^2\ge0\forall x\\ \Rightarrow N=\left(x-2y+3\right)^2+\left(y-1\right)^2+5\ge5\forall x\)

Dấu \("="\) xảy ra khi:

\(\left\{{}\begin{matrix}\left(y-1\right)^2=0\\\left(x-2y+3\right)^2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y-1=0\\x-2y+3=0\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=1\\x=2y-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=1\\x=-1\end{matrix}\right.\)

Vậy \(N_{Min}=5\) khi \(\left\{{}\begin{matrix}x=-1\\y=1\end{matrix}\right.\)

Answer 2

[Trần Quốc Lộc]

\(\text{a) Ta có : }\widehat{DMA}=90^0\left(DM\perp AB\right)\\ \widehat{DNA}=90^0\left(DN\perp AC\right)\\ \widehat{MAN}=90^0\left(gt\right)\\ \Rightarrow\text{Tứ giác }AMDN\text{ có }:\widehat{DMA}=\widehat{DNA}=\widehat{MAN}=90^0\\ \Rightarrow\text{Tứ giác }AMDN\text{ là hình chữ nhật }\left(\text{Dấu hiệu nhận biết}\right)\)

\(\text{b) Ta có : }AH\perp BC\left(gt\right)\Rightarrow AD\ge AH\left(Tính\text{ chất đường xiên}\right)\\\text{Mà }AD=MN\left(\text{Tính chất đường chéo hình chữ nhật}\right)\\ \Rightarrow MN\ge AH\)

Dấu "='' xảy ra khi:

\(AH\equiv AD\Rightarrow H\equiv D\)

Vậy đoạn thẳng MN nhận giá trị nhỏ nhất khi \(H\equiv D\)