giải câu b 
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi giao điểm AE và BP là F;
Gọi giao điểm QD và AB là H;
Gọi kéo dài AD cắt BF tại P'
Dễ cm M là trung điểm AC
Xét \(\Delta OMC\) có QD//CM\(\Rightarrow\dfrac{OD}{OM}=\dfrac{QD}{CM}\)(hệ quả tales)
Tương tự với \(\Delta OAM\) có \(\dfrac{OD}{OM}=\dfrac{DH}{AM}\)
\(\Rightarrow\dfrac{QD}{CM}=\dfrac{DH}{AM}\)
Mà CM=AM (vì M là tđ AC)
\(\Rightarrow QD=DH\)
Dễ cm P là trung điểm BF
Xét \(\Delta ABP'\) có DH//BP'
\(\Rightarrow\dfrac{DH}{BP'}=\dfrac{AD}{AP'}\)(tales)
Tương tự với \(\Delta AFP'\) có \(\dfrac{QD}{FP'}=\dfrac{AD}{AP'}\)
\(\Rightarrow\dfrac{DH}{BP'}=\dfrac{QD}{FP'}\)
Mà DH=QD (cmt)
\(\Rightarrow BP'=FP'\)
\(\Rightarrow\)P' là trung điểm BF
\(\Rightarrow P\equiv P'\)
\(\Rightarrow A,D,P\) thẳng hàng

b: (d) cắt trục tung tại điểm có tung độ là -3 và cắt trục hoành tại điểm có hoành độ là 2
Gọi (d): y=ax+b(a<>0) là phương trình đường thẳng cần tìm
Vì (d) cắt trục tung tại điểm có tung độ là -3 nên thay x=0 và y=-3 vào (d), ta được:
\(a\cdot0+b=-3\)
=>b=-3
=>(d): y=ax-3
Vì (d) cắt trục hoành tại điểm có hoành độ là 2 nên thay x=2 và y=0 vào (d), ta được:
\(2\cdot a-3=0\)
=>2a-3=0
=>2a=3
=>\(a=\dfrac{3}{2}\)
Vậy: (d): \(y=\dfrac{3}{2}x-3\)

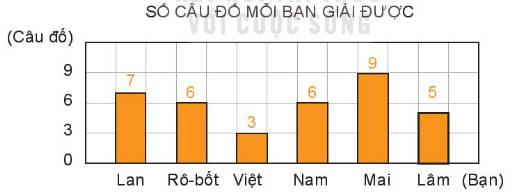
a) Trong số 6 bạn, bạn Mai giải được nhiều câu đố nhất. Bạn Việt giải được ít câu đố nhất.
b) 6 bạn đã giải được tất cả số câu đố là: 7 + 6 + 3 + 6 + 9 + 5 = 36 (câu đố)
c) Trung bình mỗi bạn giải được số câu đố là: (7 + 6 + 3 + 6 + 9 + 5) : 6 = 6 (câu đố)



Phương trình đường thẳng d' qua M và vuông góc \(\Delta\) (nên nhận \(\left(1;1\right)\) là 1 vtpt) có dạng:
\(1\left(x-3\right)+1\left(y-2\right)=0\Leftrightarrow x+y-5=0\)
Gọi H là giao điểm d' và \(\Delta\Rightarrow\) tọa độ H là nghiệm:
\(\left\{{}\begin{matrix}x-y=0\\x+y-5=0\end{matrix}\right.\) \(\Rightarrow H\left(\dfrac{5}{2};\dfrac{5}{2}\right)\)
M' là ảnh của M qua phép đối xứng trục \(\Rightarrow\) H là trung điểm MM'
\(\Rightarrow\left\{{}\begin{matrix}x_{M'}=2x_H-x_M=2\\y_{M'}=2y_H-y_M=3\end{matrix}\right.\) \(\Rightarrow M'\left(2;3\right)\)
Gọi \(d_1\) là ảnh của d qua phép đối xứng trục
Gọi A là giao điểm d và \(\Delta\Rightarrow A\in d_1\), tọa độ A thỏa mãn:
\(\left\{{}\begin{matrix}x+4y-3=0\\x-y=0\end{matrix}\right.\) \(\Rightarrow A\left(\dfrac{3}{5};\dfrac{3}{5}\right)\)
Lấy \(B\left(3;0\right)\) là 1 điểm thuộc d
Phương trình đường thẳng \(\Delta'\) qua B và vuông góc \(\Delta\) có dạng:
\(1\left(x-3\right)+1\left(y-0\right)=0\Leftrightarrow x+y-3=0\)
Gọi C là giao điểm \(\Delta\) và \(\Delta'\Rightarrow\) tọa độ C thỏa mãn:
\(\left\{{}\begin{matrix}x+y-3=0\\x-y=0\end{matrix}\right.\) \(\Rightarrow C\left(\dfrac{3}{2};\dfrac{3}{2}\right)\)
B' là ảnh của B qua phép đối xứng trục \(\Delta\Rightarrow B'\in d_1\) và C là trung điểm BB'
\(\Rightarrow\left\{{}\begin{matrix}x_{B'}=2x_C-x_B=0\\y_{B'}=2y_C-y_B=3\end{matrix}\right.\) \(\Rightarrow B'\left(0;3\right)\)
\(\Rightarrow\overrightarrow{AB'}=\left(-\dfrac{3}{5};\dfrac{12}{5}\right)=\dfrac{3}{5}\left(-1;4\right)\)
\(\Rightarrow d_1\) nhận (4;1) là 1 vtpt
Phương trình \(d_1\):
\(4\left(x-0\right)+1\left(y-3\right)=0\Leftrightarrow4x+y-3=0\)

1: Xét ΔABE vuông tại B và ΔADC vuông tại D có
\(\widehat{AEB}=\widehat{ACD}\)
Do đó: ΔABE∼ΔADC
Suy ra: \(\dfrac{AB}{AD}=\dfrac{AE}{AC}\)
hay \(AB\cdot AC=AE\cdot AD\)

2:
b: Khi x=-3 thì (1) sẽ là -3(m-1)+2m+5=0
=>-3m+3+2m+5=0
=>8-m=0
=>m=8
c: Để ptvn thì m-1=0
=>m=1

1) những giải pháp đang được sử dụng để cải tạo hoang mạc là:
- Cải tảo đất
-Phát triển hệ thống thủy lợi
-Trồng rừng
-Giảm sự gia tăng dân số








a) Số học sinh còn lại thích học văn hoặc toán hoặc cả văn lẫn toán: 95
Ví số học sinh thích học toán là 75 => số học sinh chỉ thích học văn là 95-75 = 20
Số học sinh thích học cả văn và toán là 60 - 20 = 40
b) Có nhiều nhất 60 học sinh thích học cả văn và toán
c) Có ít nhất 35 hs thích học cả văn và toán