Cho P(x) = ax2 + bx + c luôn bằng 0 với mọi x bất kì. Chứng minh rằng a = b = c = 0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
15 tháng 6 2023
Vì PTVN nên Δ<0
=>f(x)=ax^2+bx+c luôn cùng dấu với a
=>f(x)>0 với mọi x
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 3 2021
\(f\left(0\right)=c⋮3\) ;
\(f\left(1\right)=a+b+c⋮3\) mà \(c⋮3\Rightarrow a+b⋮3\)
\(f\left(-1\right)=a-b+c=-2b+\left(a+b+c\right)⋮3\) mà \(a+b+c⋮3\Rightarrow-2b⋮3\Rightarrow b⋮3\) (do 2 và 3 nguyên tố cùng nhau)
\(\left\{{}\begin{matrix}a+b+c⋮3\\b⋮3\\c⋮3\end{matrix}\right.\) \(\Rightarrow a⋮3\)
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 3 2021
Đặt \(f\left(x\right)=x^3+ax^2-bx+c\)
\(\lim\limits_{x\rightarrow+\infty}\left(x^3+ax^2-bx+c\right)=\lim\limits_{x\rightarrow+\infty}x^3\left(1+\dfrac{a}{x}-\dfrac{b}{x^2}+\dfrac{c}{x^3}\right)=+\infty\)
\(\Rightarrow\) Luôn tồn tại \(x=m>0\) đủ lớn sao cho \(f\left(m\right)>0\)
\(\lim\limits_{x\rightarrow-\infty}\left(x^3+ax^2-bx+c\right)=\lim\limits_{x\rightarrow-\infty}x^3\left(1-\dfrac{a}{x}+\dfrac{b}{x^2}+\dfrac{c}{x^3}\right)=-\infty\)
\(\Rightarrow\) Luôn tồn tại \(x=n< 0\) đủ nhỏ sao cho \(f\left(n\right)< 0\)
\(\Rightarrow f\left(m\right).f\left(n\right)< 0\Rightarrow f\left(x\right)=0\) luôn có nghiệm
15 tháng 4 2022
\(Q\left(0\right)=c⋮2014⋮1007\)
\(Q\left(1\right)=\left(a+b+c\right)⋮2014\Rightarrow\left(a+b\right)⋮2014\Rightarrow\left(2a+2b\right)⋮2014\)
\(Q\left(2\right)=\left(4a+2b+c\right)⋮2014\Rightarrow\left(4a+2b\right)⋮2014\)
\(\Rightarrow\left(4a+2b-2a-2b\right)⋮2014\)
\(\Rightarrow2a⋮2014\Rightarrow a⋮1007\Rightarrow b⋮1007\)
\(\Rightarrowđpcm\)
TT
0
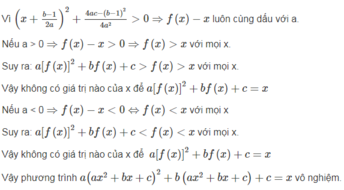
với mọi giá trị của x thì ax2 + bx + c = 0
nên ta có thể lấy giá trị của x bất kỳ
với x = 0 => ax2 + bx + c = 0 <=> c = 0 => ax2 + bx = 0
với x = 1 => ax2 + bx = 0 <=> a + b = 0 (1)
với x = -1 => ax2 + bx = 0 <=> a-b = 0 (2)
từ (1) và (2) => 2a = 0 => a = 0
=> b = 0
vậy a = b = c = 0
f(x) = 0 với mọi giá trị của x, ta chọn:
x = 0 => ax2+bx+c = c = 0
x = 1 => a+b +c = 0
x = -1 => a - b + c = 0
=> 2b = 0 => b = 0
=> a = b = c = 0
------------
phương trình đa thức bậc n có nhiều hơn n nghiệm <=> các hệ số bằng nhau và = 0