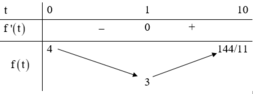
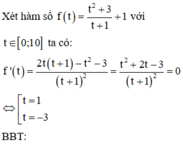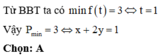Cho x + y = 1, tìm Giá trị nhỏ nhất biết C = 3x2 + 3y2 + 2018/9xy
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


3x^2+3y^2+4xy-2x+2y+2=0
=>2x^2+4xy+2y^2+x^2-2x+1+y^2+2y+1=0
=>x=1 và y=-1
M=(1-1)^2017+(1-2)^2018+(-1+1)^2015=1


\(A=3x^2+3y^2+z^2\ge0;\forall x,y,z\in R\)Dấu ''='' xảy ra khi x = y = z = 0
Vậy minA = 0 khi x = y = z = 0

Đáp án C
f x = − x 3 − 3 x 2 + m ⇒ f ' x = − 3 x 2 − 6 x f ' x = 0 ⇔ x = 0 x = − 2 ( l o a i )
Tại x=0, ta có y 0 = m ⇒ y 0 = 0 ⇔ m = 0
Chọn phương án C.

E = 2 x 3 – 2 y 3 – 3 x 2 – 3 y 2 = 2 ( x 3 – y 3 ) – 3 ( x 2 + y 2 ) = 2 ( x – y ) ( x 2 + x y + y 2 ) – 3 ( x 2 + y 2 )
Vì x – y = 1 nên
E = 2 ( x 2 + y 2 + x y ) – 3 x 2 – 3 y 2 = - ( x 2 – 2 x y + y 2 ) = - ( x – y ) 2 = - 1
Đáp án cần chọn là: A

Bài 1:
Ta thấy: $(x+\frac{1}{2})^2\geq 0$ với mọi $x\in\mathbb{R}$
$\Rightarrow (x+\frac{1}{2})^2+\frac{5}{4}\geq \frac{5}{4}$
Vậy gtnn của biểu thức là $\frac{5}{4}$
Giá trị này đạt tại $x+\frac{1}{2}=0\Leftrightarrow x=-\frac{1}{2}$
Bài 2:
$x+y-3=0\Rightarrow x+y=3$
\(M=x^2(x+y)-(x+y)x^2-y(x+y)+4y+x+2019\)
\(=-3y+4y+x+2019=x+y+2019=3+2019=2022\)