1 người đi xe đạp nửa quảng đường đầu V1= 12km/h, nửa quãng đường sau đi với V2. Biết vận tốc trung bình cả quảng đường là 8km/h. Tính V2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
24 tháng 10 2023
Gọi nửa quãng đường là S
\(t_1\) là thời gian đi hết nửa quãng đường đầu
\(t_1=\dfrac{s}{12}\)
\(t_2\) là thời gian đi hết nửa quãng đường sau
\(t_2=\dfrac{S}{v_2}\)
\(v_{tb}=\dfrac{S+S}{t_1+t_2}=\dfrac{2S}{\dfrac{S}{12}+\dfrac{S}{v_2}}=8\)
\(\Leftrightarrow\dfrac{2S}{\dfrac{S\left(12+v_2\right)}{12v_2}}=8\Leftrightarrow\dfrac{24v_2}{12+v_2}=8\Rightarrow v_2=6\) km/h
15 tháng 6 2021
Gọi s là chiều dài nửa quãng đường mà người đi xe đạp phải đi.
Như vậy, thời gian đi hết nửa quãng đường đầu s1 = s với vận tốc v1 là:
Thời gian đi hết nửa quãng đường còn lại s2 = s với vận tốc v2 là:
Vậy tổng thời gian đi hết cả quãng đường là: 
Vận tốc trung bình của người đi xe đạp trên cả quãng đường là:
15 tháng 6 2021
Giải
Gọi s là chiều dài nửa quãng đường
Thời gian đi hết nửa quãng đường đầu với vận tốc v1 là t1=s/v1 (1)
Thời gian đi hết nửa quãng đường còn lại với vận tốc v2 là t2=s/v2 (2)
Vận tốc trung bình của người đi xe đạp trên quãng đường là vtb = 2s/t1+ t2 (3)
Kết hợp (1); (2); (3) có: 1/v1 + 1/v2 = 2/vtb
Thay số vtb = 8km/h ; v1 = 12km/h
Vận tốc trung bình của người đi xe ở nửa quãng đường sau là v2 = 6km/h.
27 tháng 12 2021
Thời gian đi nửa quãng đường đầu:
\(t_1=\dfrac{S_1}{v_1}=\dfrac{\dfrac{1}{2}S}{12}=\dfrac{S}{24}h\)
Thời gian đi nửa quãng đường sau:
\(t_2=\dfrac{S_2}{v_2}=\dfrac{\dfrac{1}{2}S}{20}=\dfrac{S}{40}h\)
Vận tốc trung bình:
\(v_{tb}=\dfrac{S_1+S_2}{t_1+t_2}=\dfrac{S}{\dfrac{S}{24}+\dfrac{S}{40}}=15\)km/h
S8
23 tháng 11 2022
Thời gian đi quãng đường đầu và quãng đường sau là:
⎧⎪ ⎪ ⎪⎨⎪ ⎪ ⎪⎩t1=S1v1=S2v1=S24(h)t2=S2v2=S2v2=S40(h){t1=S1v1=S2v1=S24(h)t2=S2v2=S2v2=S40(h)
Vận tốc trung bình là: vtb=S1+S2t1+t2=SS24+S40=SS(124+140)=15(kmh)vtb=S1+S2t1+t2=SS24+S40=SS(124+140)=15(kmh)
VT
7 tháng 11 2017
Gọi s là chiều dài nửa quãng đường mà người đi xe đạp phải đi.
Như vậy, thời gian đi hết nửa quãng đường đầu s1 = s với vận tốc v1 là:
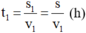
Thời gian đi hết nửa quãng đường còn lại s2 = s với vận tốc v2 là:
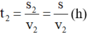
Vậy tổng thời gian đi hết cả quãng đường là: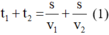 
Vận tốc trung bình của người đi xe đạp trên cả quãng đường là:
DN
5 tháng 7 2017
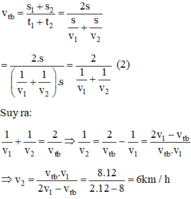
Vận tốc người đi xe đạp đi nửa quãng đường còn lại là:
\(v_{tb}=\dfrac{2}{\dfrac{1}{12}+\dfrac{1}{v_2}}=\dfrac{2}{\dfrac{1}{4}}=8\left(\dfrac{km}{h}\right)\)
=> \(\dfrac{1}{4}-\dfrac{1}{12}=\dfrac{1}{6}\) => \(v_2=6\left(\dfrac{km}{h}\right)\)
Đáp số: 6 km/h.
30 tháng 6 2016
Vtb = (S1 + S2)/(t1 + t2)=2S1/(S1/V1 + S2/V2) = 2/(1/V1 + 1/V2) ( cùng rút gọn cho S1)
<=> 8 = 2/(1/12 + 1/V2) => V2 = 6 (km/h)
Vậy vận tốc trên quãng đường còn lại là 6km/h.
16 tháng 11 2021
Thời gian đi nửa quãng đường đầu:
\(t_1=\dfrac{S_1}{v_1}=\dfrac{\dfrac{1}{2}S}{2}=\dfrac{S}{4}s\)
Thời gian đi nửa quãng đường sau:
\(t_2=\dfrac{S_2}{v_2}=\dfrac{\dfrac{1}{2}S}{v_2}=\dfrac{\dfrac{1}{2}S}{3}=\dfrac{S}{6}s\)
Vận tốc trung bình:
\(v_{tb}=\dfrac{S}{t_1+t_2}=\dfrac{S}{\dfrac{S}{4}+\dfrac{S}{6}}=\dfrac{S}{\dfrac{5S}{12}}=2,4\)(m/s)
DQ
24 tháng 12 2020
Thời gian người đó đi nửa quãng đường đầu và nửa quãng đường sau lần lượt là:
\(t_1=\dfrac{s_1}{v_1}=\dfrac{s}{2v_1}\)
\(t_2=\dfrac{s_2}{v_2}=\dfrac{s}{2v_2}\)
Tốc độ trung bình trên cả đoạn đường là:
\(v=\dfrac{s_1+s_2}{t_1+t_2}=\dfrac{s}{\dfrac{s}{2v_1}+\dfrac{s}{2v_2}}=\dfrac{1}{\dfrac{1}{2v_1}+\dfrac{1}{2v_2}}\)
Thay số ta được:
\(v=\dfrac{1}{\dfrac{1}{2.15}+\dfrac{1}{2.20}}=17,14\) (km/h)
Tham khảo
Vtb = (S1 + S2)/(t1 + t2)=2S1/(S1/V1 + S2/V2) = 2/(1/V1 + 1/V2) ( cùng rút gọn cho S1)
<=> 8 = 2/(1/12 + 1/V2) => V2 = 6 (km/h)
Vậy vận tốc trên quãng đường còn lại là 6km/h.
\(v_{tb}=\dfrac{1}{\dfrac{\dfrac{1}{2}}{v_1}+\dfrac{\dfrac{1}{2}}{v_2}}\\ \Leftrightarrow8=\dfrac{1}{\dfrac{\dfrac{1}{2}}{12}+\dfrac{\dfrac{1}{2}}{v_2}}\\ \Leftrightarrow8=\dfrac{1}{\dfrac{1}{24}+\dfrac{1}{2v_2}}\\ \Leftrightarrow8.\left(\dfrac{1}{24}+\dfrac{1}{2v_2}\right)=1\\ \Leftrightarrow\dfrac{1}{2v_2}=\dfrac{1}{8}-\dfrac{1}{24}=\dfrac{1}{12}\\ \Leftrightarrow v_2=\dfrac{1.12}{2.1}=6\left(\dfrac{km}{h}\right)\)