\(\Delta ABC\) vuông tại A. Đường cao AH = 24cm. AB:AC = 3:4. BH, CH = ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1 / xét tam giác ABH đồng dạng vs CAH trg hợp g-g suy ra AB/AC =BH/AH
<=> 3 /7 =BH /42
=> BH =18 cm
2 áp dụng hệ thức lượng AH^2 =BH .CH từ bh/ch =9/16 =>CH= 16BH/9
TA CÓ AH ^2 =16BH^2 /9 SUY RA BH =36 cm SUY RA CH = 64 cm áp dụng pita go suy ra AB ,AC hoặc hệ thức lg cũng đc

Lời giải:
Vì $AB:AC=3:4$ nên đặt $AB=3a; AC=4a$ với $a>0$
Áp dụng định lý Pitago:
$AB^2+AC^2=BC^2$
$\Leftrightarrow (3a)^2+(4a)^2=225$
$\Leftrightarrow 25a^2=225$
$\Rightarrow a=3$ (do $a>0$)
Áp dụng hệ thức lượng trong tam giác vuông:
$AB^2=BH.BC\Rightarrow BH=\frac{AB^2}{BC}=\frac{9a^2}{15}=\frac{9.3^2}{15}=5,4$ (cm)
$AC^2=CH.CB\Rightarrow CH=\frac{AC^2}{BC}=\frac{16a^2}{15}=\frac{16.3^2}{15}=9,6$ (cm)

Lời giải:
Do $AB:AC=3:4$ nên đặt $AB=3a; AC=4a$ với $a>0$
Áp dụng hệ thức lượng trong tam giác vuông:
$\frac{1}{144}=\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}=\frac{1}{(3a)^2}+\frac{1}{(4a)^2}=\frac{25}{144a^2}$
$\Rightarrow a^2=25\Rightarrow a=5$ (do $a>0$)
$\Rightarrow AB=3a=15; AC=4a=20$ (cm)
$BH=\sqrt{AB^2-AH^2}=\sqrt{15^2-12^2}=9$ (cm)
$CH=\sqrt{AC^2-AH^2}=\sqrt{20^2-12^2}=16$ (cm) - theo định lý Pitago

Sử dụng hệ thức về cạnh góc vuông và đường cao trong tam giác vuông, tính được BH =4,5cm, CH = 8cm

Ta có: \(\dfrac{AB}{AC}=\dfrac{3}{4}\)
nên \(AB=\dfrac{3}{4}AC\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)
\(\Leftrightarrow\dfrac{1}{\dfrac{9}{16}AC^2}+\dfrac{1}{AC^2}=\dfrac{1}{576}\)
\(\Leftrightarrow AC^2\cdot\dfrac{9}{16}=576\cdot\dfrac{25}{16}=900\)
\(\Leftrightarrow AC^2=1600\left(cm\right)\)
\(\Leftrightarrow AC=40\left(cm\right)\)
\(\Leftrightarrow AB=30\left(cm\right)\)
\(\Leftrightarrow BC=50cm\)

Ta có: \(\dfrac{AB}{AC}=\dfrac{3}{4}\)
nên \(AB=\dfrac{3}{4}\cdot AC=\dfrac{3}{4}\cdot14=10.5\left(cm\right)\)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=10.5^2+14^2=306.25\)
hay BC=17,5(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=\dfrac{AB^2}{BC}=\dfrac{10.5^2}{17.5}=6,3\left(cm\right)\\CH=\dfrac{AC^2}{BC}=\dfrac{14^2}{17.5}=11.2\left(cm\right)\end{matrix}\right.\)
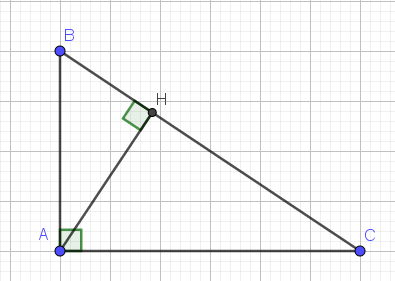

Ta có: \(\dfrac{AB}{AC}=\dfrac{3}{4}\)
\(\Leftrightarrow\dfrac{HB}{HC}=\dfrac{9}{16}\)
\(\Leftrightarrow HB=\dfrac{9}{16}\cdot HC\)
Ta có: \(AH^2=HB\cdot HC\)
\(\Leftrightarrow HC^2\cdot\dfrac{9}{16}=24^2\)
\(\Leftrightarrow HC=32\left(cm\right)\)
hay HB=18(cm)