Cho đường tròn ( O ) đường kính AB = 2R . Từ trung điểm I của đoạn OA vẽ dây cung CD vuông góc với AB . Trên cung nhỏ BC lấy điểm M tùy ý , AM cắt CD tại N .
1/ Chứng minh tứ giác BMNI nội tiếp .
2/ Vẽ tiếp tuyến tại M của đường tròn ( O ) cắt tia DC tại E và tia AB tại F .
a/ Chứng minh tam giác EMN cân .
b/ Chứng minh AN . AM = R2
3/ Gỉa sử \(\widehat{MAB}\) = 300 . Tính diện tích giới hạn bởi cung nhỏ MB...
Đọc tiếp
Cho đường tròn ( O ) đường kính AB = 2R . Từ trung điểm I của đoạn OA vẽ dây cung CD vuông góc với AB . Trên cung nhỏ BC lấy điểm M tùy ý , AM cắt CD tại N .
1/ Chứng minh tứ giác BMNI nội tiếp .
2/ Vẽ tiếp tuyến tại M của đường tròn ( O ) cắt tia DC tại E và tia AB tại F .
a/ Chứng minh tam giác EMN cân .
b/ Chứng minh AN . AM = R2
3/ Gỉa sử \(\widehat{MAB}\) = 300 . Tính diện tích giới hạn bởi cung nhỏ MB của đường tròn ( O ) và các đoạn MF , BF theo R .
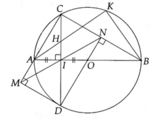
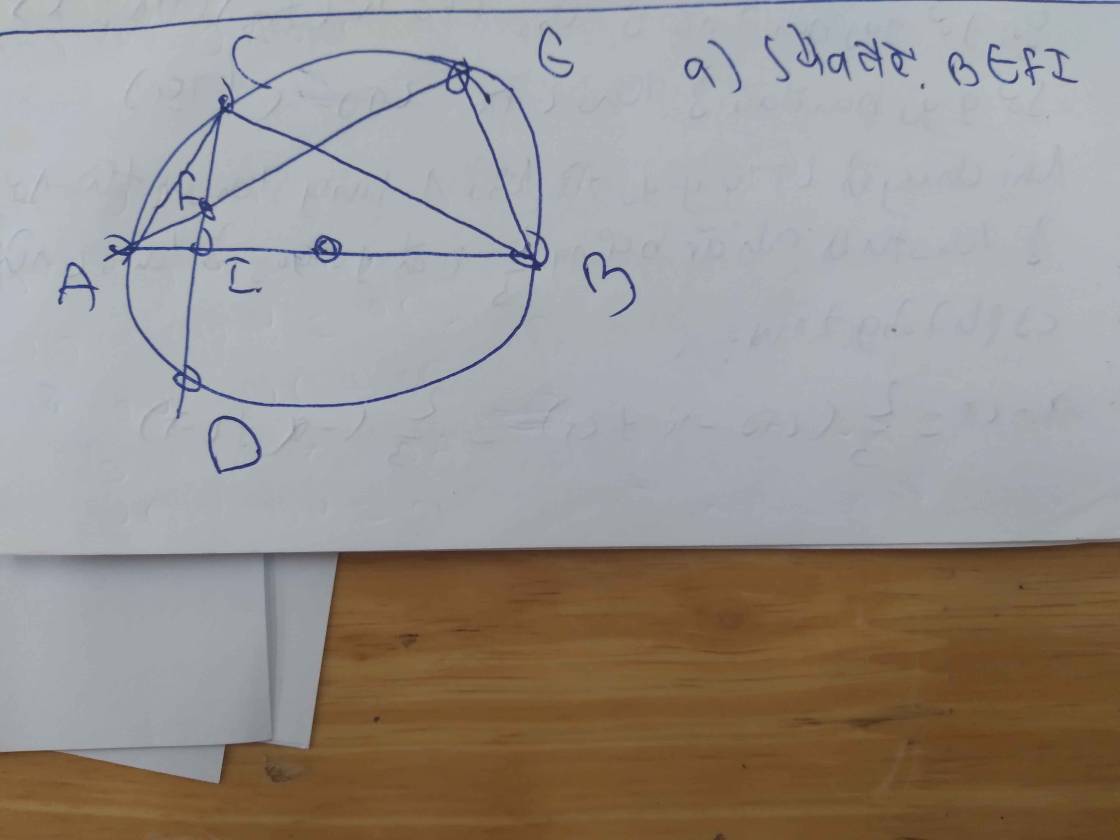
1) \(NMB = NIB = 90^o\)
2) a. \(EMN = MBA = \dfrac{\stackrel\frown{AM}}{2}\) (1)
\(MBA = MNE\) (do BMNT nội tiếp) (2)
\((1) + (2) \Rightarrow EMN = MNE\)
b. nối NO
△ANO cân => NAO = NOA = AMO
△ANO ~ △AOM (g.g) => \(\dfrac{AO}{AM} = \dfrac{AN}{OM}\)
\(\Rightarrow AM.AN = AO.OM = R^2\)
3) \(MAB = 30^o \Rightarrow AMO = 30^o \Rightarrow OMB = 90^o - 30^o = 60^o \)
=> tam giác OMB đều => MB= OB = OM = R
Có:
\(\begin{cases} BMF = 90^o - 60^o = 30^o \\ BFM = 90^o - 60^o = 30^o \end{cases}\)=> △MBF cân tại B
=> MB = BF = R => OF = OB + BF = R+ R = 2R
Tam giác OMF có: \(MF^2 = OF^2 - OM^2 = 3R^2\)
Câu 3 ý 1 tớ ko hiểu đề nên tớ ko làm!!! Còn một số chỗ tắt nhưng dễ hiểu lắm, tớ rút gọn đi nha
Các bạn ơi giúp mình với , mình sắp thi rồi