Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) Ta có: AB⊥AC(ΔABC vuông tại A)
HK⊥AC(Gt)
Do đó: AB//HK(Định lí 1 từ vuông góc tới song song)
b) Xét ΔAKH vuông tại H và ΔAIH vuông tại H có
KH=IH(gt)
AH chung
Do đó: ΔAKH=ΔAIH(hai cạnh góc vuông)
Suy ra: AK=AI(hai cạnh tương ứng)
Xét ΔAKI có AK=AI(cmt)
nên ΔAKI cân tại A(Định nghĩa tam giác cân)
a) sử dụng tc: Từ vuông góc đến //
b)tam giác KHA= tam giác IHA(c.g.c)
=> AK=AI
=> góc AKI=góc AIK
vì AK=AI=> tam giác AKI cân
c) vì AB//HK=> góc BAK=góc AKI(so le trong)
góc BAK=góc AKI
mà góc AKI=góc AIK(cmt)
d) vì HC vuông góc với KI, KH=HI( GT) =>HC là trung trực=> KC=CI( t/c đường trung trực
tam giác AKC = tam giác AIC(c.c.c)
mk vẽ ko có kí hiệu bn thông cảm
a) dễ thấy AB // HK ( vì cùng vuông góc với AC)
b) Vì \(AC\perp KI\)tại H và \(HK=HI\)nên AC là đường trung trực của KI
hay AH là đường trung trực của HI hay tam giác AKI cân tại A
c) Vì tam giác AKI cân tại A nên \(\widehat{AKI}=\widehat{AIK}\)
Mà \(\widehat{BAK}=\widehat{AKI}\)(2 góc so le trong)
=> \(\widehat{AIK}=\widehat{BAK}\)
a/ Ta có
\(AB\perp AC\left(gt\right)\)
\(HK\perp AC\left(gt\right)\)
=> AB//HK (cùng vuông góc với AC)
b/ Xét tg AKI có
\(AH\perp HI\) => AH là đường cao của tg AKI
HK=HI (gt) => AH là trung tuyến của tg AKI
=> tg AKI cân tại A (Tam giác có đường cao đồng thời là đường trung tuyến thì tg đó là tg cân)
c/ Ta có
tg AKI cân tại A \(\Rightarrow\widehat{AIK}=\widehat{AKI}\) (góc ở đáy tg cân)
AB//HK (cmt) \(\Rightarrow\widehat{BAK}=\widehat{AKI}\) (góc so le trong)
\(\Rightarrow\widehat{BAK}=\widehat{AIK}\) (cùng bằng góc \(\widehat{AKI}\) )
d/ Xét tg CKI có
\(CH\perp KI\) => CH là đường cao của tg CKI
HK=HI => CH là trung tuyến của tg CKI
=> tg CKI cân tại C (Tam giác có đường cao đồng thời là đường trung tuyến thì tg đó là tg cân)
Xét tg AIC và tg AKC có
tg AKI cân tại A (cmt) => AI=AK
tg CKI cân tại C (cmt) => CI=CK
AC chung
=> tg AIC = tg AKC (c.c.c)
a: Ta có: AB\(\perp\)AC
IK\(\perp\)AC
Do đó: IK//AB
b: Xét ΔAKH vuông tại H và ΔAIH vuông tại H có
AH chung
HK=HI
Do đó: ΔAKH=ΔAIH
Suy ra: AK=AI
Xét ΔAKI có AK=AI
nên ΔAKI cân tại A
c: Ta có: \(\widehat{BAK}+\widehat{HAK}=90^0\)
\(\widehat{AIK}+\widehat{HAI}=90^0\)
mà \(\widehat{HAK}=\widehat{HAI}\)
nên \(\widehat{BAK}=\widehat{AIK}\)
có hình ko
a) sử dụng tc: Từ vuông góc đến //
b)tam giác KHA= tam giác IHA(c.g.c)
=> AK=AI
=> góc AKI=góc AIK
vì AK=AI=> tam giác AKI cân
c) vì AB//HK=> góc BAK=góc AKI(so le trong)
}=> góc BAK=góc AIK
mà góc AKI=góc AIK(cmt)
d) vì HC vuông góc với KI, KH=HI( GT) =>HC là trung trực=> KC=CI( t/c đường trung trực
tam giác AKC = tam giác AIC(c.c.c)
Hết
đúng nha
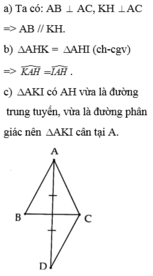
a: Ta co: HK\(\perp\)AC
AB vuông góc với AC
Do đó: HK//AB
b: Xét ΔAKI có
AH là đường cao
AH là đường trung tuyến
Do đó: ΔAKI cân tại A
d: Xét ΔAIC và ΔAKC có
AI=AK
góc IAC=góc KAC
AC chung
Do đó: ΔAIC=ΔAKC