TÌM X BIẾT: 2x+2_ 2x= 96
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
9 tháng 3 2019
Xét cấp số cộng 1, 6, 11, ..., 96.
Ta có: 96 = 1 + 5(n − 1) ⇒ n = 20
Suy ra
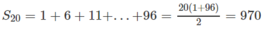
Và 2x.20 + 970 = 1010
Từ đó x = 1
10 tháng 9 2023
a: Ta sẽ có hình vẽ sau:
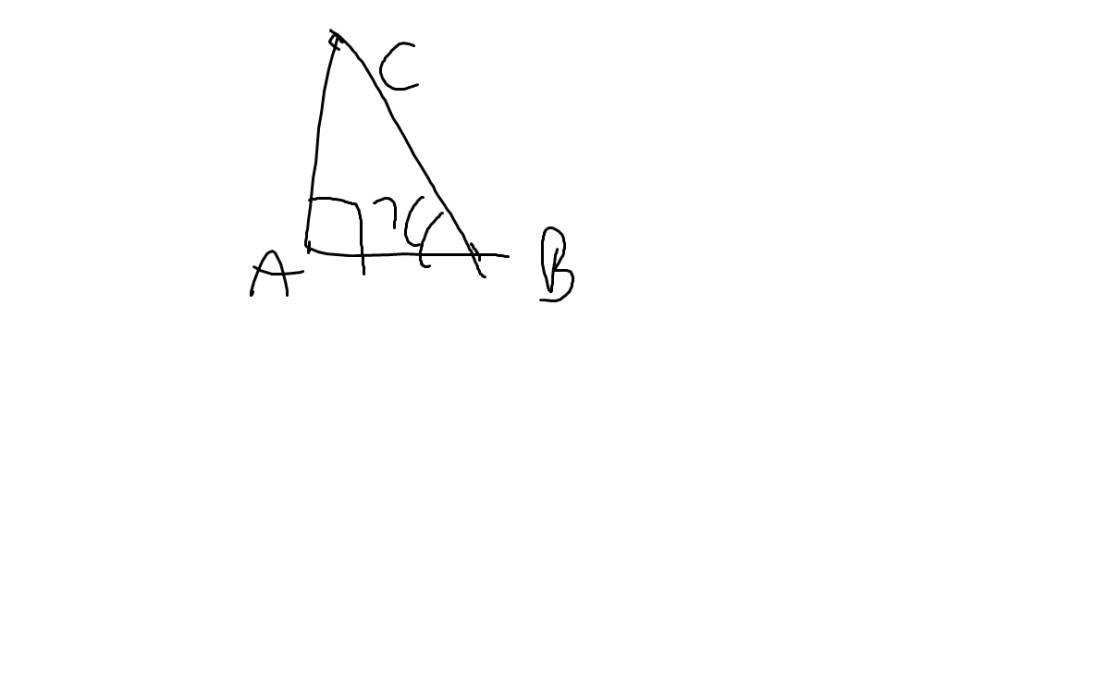
Đặt \(x=\widehat{B}\)
sin x=sin B=AC/BC
cosx=cosB=AB/BC
\(tanx=tanB=\dfrac{AC}{AB}=\dfrac{sinx}{cosx}\)
=>\(tan^2x=\dfrac{sin^2x}{cos^2x}\)
b: \(cot^2x=\dfrac{1}{tan^2x}=1:\dfrac{sin^2x}{cos^2x}=\dfrac{cos^2x}{sin^2x}\)
KW
0
NP
0
23 tháng 2 2019
Sửa đề :
Tìm GTNN của \(A=\frac{x^2-2x+2011}{x^2}\)
Giải :
\(A=\frac{x^2-2x+2011}{x^2}\)
\(A=\frac{x^2}{x^2}-\frac{2x}{x^2}+\frac{2011}{x^2}\)
\(A=1-\frac{2}{x}+\frac{2011}{x^2}\)
\(A=1-2\cdot\frac{1}{x}+2011\cdot\left(\frac{1}{x}\right)^2\)
Đặt \(\frac{1}{x}=a\)
\(A=1-2a+2011a^2\)
\(A=2011\left(a^2-\frac{2}{2011}a+\frac{1}{2011}\right)\)
\(A=2011\left(a^2-2\cdot a\cdot\frac{1}{2011}+\frac{1}{2011^2}+\frac{2010}{4044121}\right)\)
\(A=2011\left[\left(a-\frac{1}{2011}\right)^2+\frac{2010}{4044121}\right]\)
\(A=2011\left(a-\frac{1}{2011}\right)^2+\frac{2010}{2011}\ge\frac{2010}{2011}\forall a\)
Dấu "=" xảy ra \(\Leftrightarrow a=\frac{1}{2011}\)
Thay a ta có : \(\frac{1}{x}=\frac{1}{2011}\)
\(\Rightarrow x=2011\)
Vậy \(A_{min}=\frac{2010}{2011}\Leftrightarrow x=2011\)
10 tháng 4 2015
a) x2 - x = 0 <=> x(x - 1) = 0 <=> x = 0 hoặc x - 1 = 0 <=> x = 0 hoặc x = 1
Vậy : S = {0; 1}.
b) x2 - 2x = 0 <=> x(x - 2) <=> x = 0 hoặc x - 2 = 0 <=> x = 0 hoặc x = 2
Vậy : S = {0; 2).
(Bài này dễ mà)
LL
1
1 tháng 10 2017
Ta có : \(x^2+y^2-2x+4y+1\)
\(=\left(x^2-2x+1\right)+\left(y^2+4y+4\right)-4\)
\(A=\left(x-1\right)^2+\left(y+2\right)^2-4\)
Vì \(\left(x-1\right)^2+\left(y+2\right)^2\ge0\forall x,y\in R\)
Nên : \(A=\left(x-1\right)^2+\left(y+2\right)^2-4\ge-4\forall x,y\in R\)
Vậy \(A_{min}=-4\) khi x = 1 và y = -2
NN
25 tháng 8 2023
\(\left(2x-1\right)^2-\left(x+3\right)^2=0\)
\(=>\left(2x-1+x+3\right)\left(2x-1-x-3\right)=0\)
\(=>\left(3x+2\right)\left(x-4\right)=0\)
\(=>\left[{}\begin{matrix}3x+2=0\\x-4=0\end{matrix}\right.\)
\(=>\left[{}\begin{matrix}3x=-2\\x=4\end{matrix}\right.\)
\(=>\left[{}\begin{matrix}x=\dfrac{-2}{3}\\x=4\end{matrix}\right.\)
\(=>x\in\left\{\dfrac{-2}{3};4\right\}\)
T
25 tháng 8 2023
\(\left(2x-1\right)^2-\left(x+3\right)^2=0\)(sửa đề)
\(\Leftrightarrow\left(2x-1-x-3\right)\left(2x-1+x+3\right)=0\)
\(\Leftrightarrow\left(x-4\right)\left(3x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-4=0\\3x+2=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=4\\x=-\dfrac{2}{3}\end{matrix}\right.\)
2 x + 2 - 2x = 96
2x . 22 - 2x = 96
2x . ( 22 - 1 ) = 96
2x . (4 - 1 ) = 96
2x . 3 = 96
2x = 96 : 3
2x = 32
2x = 25
=> x = 5
Vậy x = 5