Question

[Tô Thu Huyền]

Cho Δ ABC vuông tại A, có AB=12cm, AC=16cm. Kẻ đường cao AH (H ∈ BC)

a, CM: ΔHBA và ΔABC đồng dạng

b, Tính độ dài các đoạn thẳng BC, AH

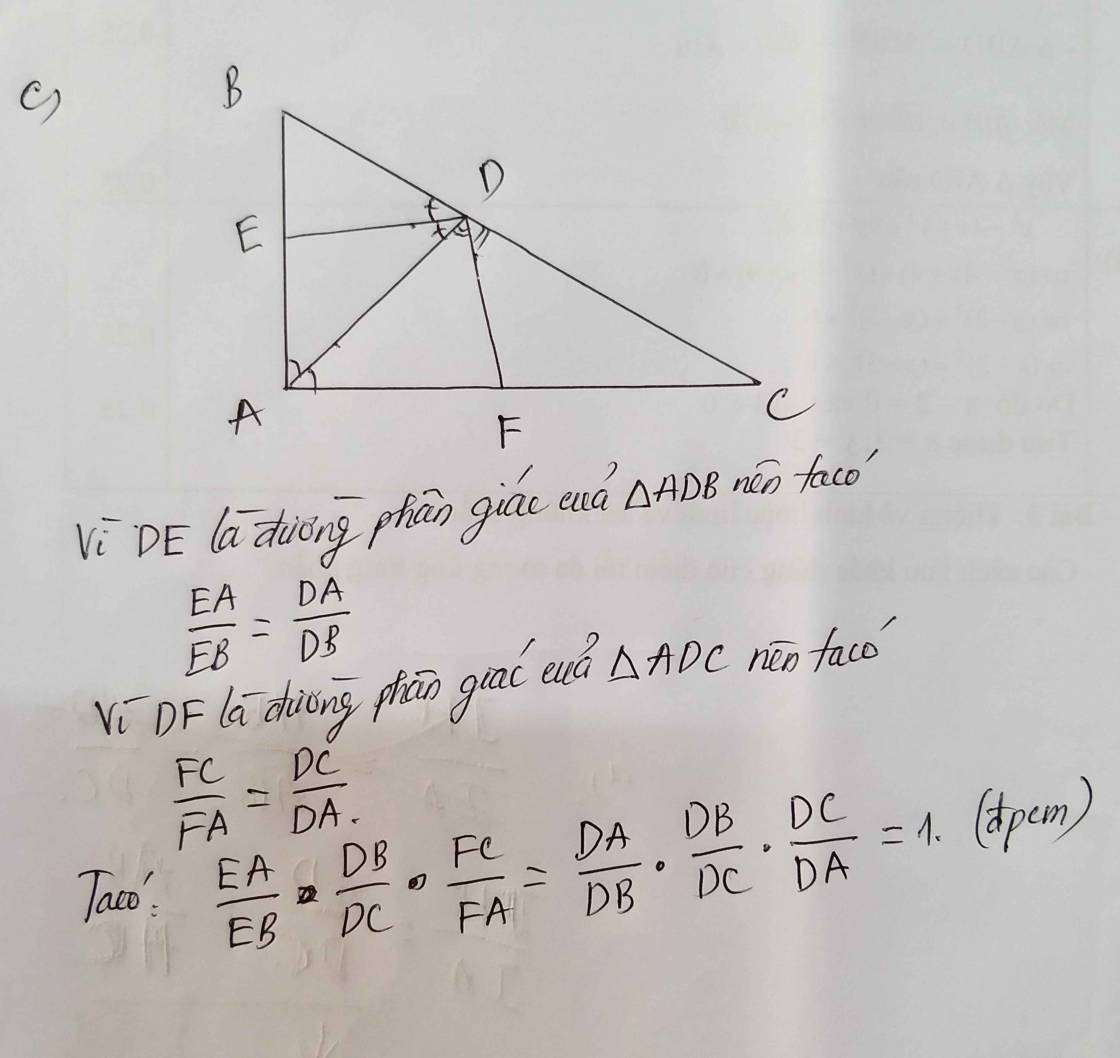
c. Trong ΔABC kẻ phân giác AD (D ∈ BC). Trong ΔADB kẻ phân giác DE (E ∈ AB), trong ΔADC kẻ phân giác DF (F ∈ AC) . CM: \(\dfrac{EA}{EB}\).\(\dfrac{DB}{DC}\).\(\dfrac{FC}{FA}\)=1

Answer 1

[Nguyễn Huế]

a) Xét\(\Delta HBA\) và\(\Delta ABC\) có:

\(\widehat{A}=\widehat{H}=90^o\left(gt\right)\)

\(\widehat{B}\) chung

\(\Rightarrow\Delta HBA\sim\Delta ABC\left(gg\right)\)

b) \(\Delta ABC\) có \(\widehat{A}=90^o\left(gt\right)\)

\(\Rightarrow BC^2=AB^2+AC^2\left(Pytago\right)\)

\(\Rightarrow BC^2=12^2+16^2\)

\(\Rightarrow BC^2=144+256\)

\(\Rightarrow BC^2=400\)

\(\Rightarrow BC=20\left(cm\right)\)

Answer 2

[Tri Nguyen]

b. Ta có: \(\Delta\)HBA \(\sim\)\(\Delta\)ABC ( cmt )

\(\dfrac{AH}{CA}=\dfrac{BA}{BC}\) \(\Leftrightarrow\dfrac{AH}{16}=\dfrac{12}{20}\Rightarrow AH=9,6\)

c. Xét \(\Delta\) ABC có: AD là đường phân giác ( gt )

\(\Rightarrow\dfrac{DB}{DC}=\dfrac{AB}{AC}\) (1)

Xét \(\Delta\) ADB có: DE là đpg ( gt )

\(\Rightarrow\dfrac{EA}{EB}=\dfrac{DA}{DB}\)(2)

Xét \(\Delta\) ADC có: DF là đpg ( gt )

\(\Rightarrow\dfrac{FC}{FA}=\dfrac{DC}{DA}\)(3)

Từ 1,2 và 3 suy ra: \(\dfrac{EA}{EB}.\dfrac{DB}{DC}.\dfrac{FC}{FA}=\dfrac{DA}{DB}.\dfrac{AB}{AC}.\dfrac{DC}{DA}\)

\(\Leftrightarrow\dfrac{EA}{EB}.\dfrac{DB}{DC}.\dfrac{FC}{FA}=\dfrac{AB}{AC}.\dfrac{DC}{DB}\)

Mà: \(\dfrac{DB}{DC}=\dfrac{AB}{AC}\) ( CM phần 1 )

\(\Rightarrow\dfrac{EA}{EB}.\dfrac{DB}{DC}.\dfrac{FC}{FA}=\dfrac{DB}{DC}.\dfrac{DC}{DB}\)

\(\Rightarrow\dfrac{EA}{EB}.\dfrac{DB}{DC}.\dfrac{FC}{FA}=1\)

Bạn tự vẽ hình nha : )