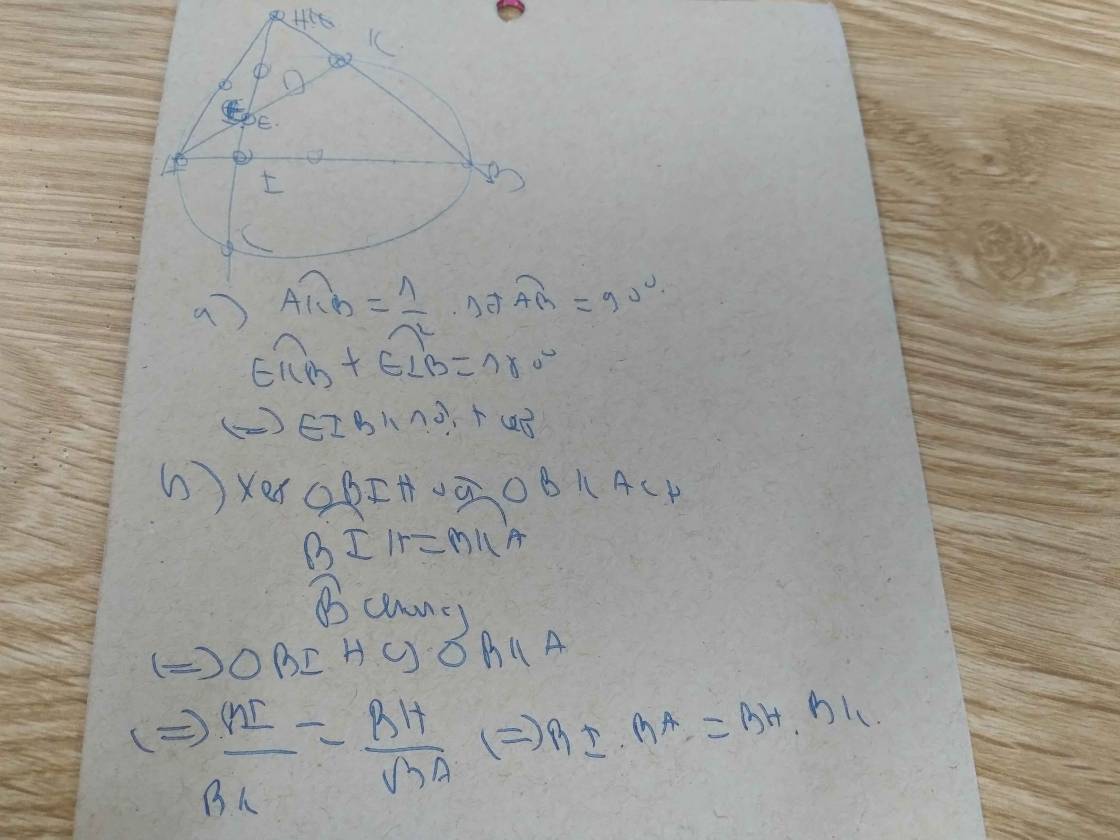cho đường tròn tâm o đường kính ab .dây cd vông góc với ab tại h .trên tia đối của tia cd lấy một điểm m ở ngoài đường tròn tâm o .kẻ mb cắt đường tròn tại điểm e.ae cắt cd tại điểm f.chứng minh rằng
a. tứ giác befh nội tiếp một đường tròn b.gọi k là giao điểm của bf với đường tròn tâm o .cm ea là tia phân giác của góc hek c.cm md.fc=mc.fdHãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chứng minh có bạn câu a,b trước. Câu c tìm không ra tam giác ~ . Chưa ra cách khác
(Vẽ đẹp hơn rồi kk)
a/ Ta có \(\widehat{AEB}=90\)độ (Góc nội tiếp chắn nửa đường tròn)
Xét tứ giác \(BEHF\)có: \(\hept{\begin{cases}\widehat{AEB}=90\left(cmt\right)\\\widehat{FHB}=90\left(gt\right)\end{cases}}\)
\(\Rightarrow\widehat{AEH}+\widehat{FHB}=90+90=180\)độ
\(\Rightarrow\)Tứ giác \(BEHF\)nội tiếp
b/ (Nối giùm mình K với A)
Ta có: \(\widehat{KEA}=\widehat{KBA}\)( Tứ giác \(KEAB\)nt, cùng chắn \(\widebat{AK}\))
Mà: \(\widehat{AEH}=\widehat{KBA}\)( Tứ giác \(BEHF\)nt, cùng chắn \(\widebat{FH}\))
\(\Rightarrow\widehat{KEA}=\widehat{AEH}\)
\(\RightarrowĐpcm\)

a) Xét (O) có
CD là dây cung(C,D∈(O))
B là điểm chính giữa của \(\stackrel\frown{CD}\)(gt)
Do đó: \(\stackrel\frown{CB}=\stackrel\frown{BD}\)
⇒\(sđ\widehat{CB}=sđ\widehat{BD}\)(1)
Xét (O) có
\(\widehat{BMD}\) là góc nội tiếp chắn cung BD(gt)
nên \(\widehat{BMD}=\dfrac{1}{2}\cdot sđ\stackrel\frown{BD}\)(Định lí góc nội tiếp)(2)
Xét (O) có
\(\widehat{BAC}\) là góc nội tiếp chắn cung BC(gt)
nên \(\widehat{BAC}=\dfrac{1}{2}\cdot sđ\widehat{CB}\)(Định lí góc nội tiếp)(3)
Từ (1), (2) và (3) suy ra \(\widehat{BMD}=\widehat{BAC}\)(đpcm)