Cho các đa thức \(F\left(x\right)=4x^2+3x-2;G\left(x\right)=3x^2-2x+5\) và \(H\left(x\right)=5x^2-2x+3\). Tìm x để \(F\left(x\right)+G\left(x\right)-H\left(x\right)=0\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) \(f\left(x\right)=2x^6+3x^2+5x^3-2x^2+4x^4-x^3+1-4x^3-x^4\)
\(f\left(x\right)=2x^6+\left(4-1\right)x^4+\left(5-1-4\right)x^3+\left(3-2\right)x^2+1\)
\(f\left(x\right)=2x^6+3x^4+x^2+1\)
b) \(2.1+3.1+1+1=7\)
c) \(\left\{{}\begin{matrix}x^6\ge0\\x^4\ge0\\x^2\ge0\end{matrix}\right.\) \(\Leftrightarrow2x^6+3x^4+x^2\ge0\Rightarrow2x^6+3x^4+x^2+1\ge1\)
=> f(x) >=1 => dpcm

f(x)=x5+3x2−5x3−x7+x3+2x2+x5−4x2−x7⇒f(x)=2x5−4x3+x2
Đa thức có bậc là 5
g(x)=x4+4x3−5x8−x7+x3+x2−2x7+x4−4x2−x8⇒g(x)=−6x8−3x7+2x4+5x3−3x2g(x)=x4+4x3−5x8−x7+x3+x2−2x7+x4−4x2−x8⇒g(x)=−6x8−3x7+2x4+5x3−3x2
Đa thức có bậc là 8.
Thu gọn và sắp xếp các đa thức f (x) và g (x) theo lũy thừa giảm của biến rồi tìm bậc của đa thức đó.

`a)P(x)+Q(x)=3x^4-x^3+4x^2+2x+1-2x^4-x^2+x-2`
`=x^4-x^3+3x^2+3x-1`
`b)Q(x)-H(x)=-2x^4-2`
`=>H(x)=Q(x)-(-2x^4-2)`
`=>H(x)=-2x^4-x^2+x-2+2x^4+2`
`=>H(x)=-x^2+x`
`c)` Cho `H(x)=0`
`=>-x^2+x=0`
`=>-x(x-1)=0`
`@TH1:-x=0=>x=0`
`@TH2:x-1=0=>x=1`
\(a,P\left(x\right)+Q\left(x\right)=x^4-x^3+3x^2+3x-1\)
\(b,H\left(x\right)=Q\left(x\right)+2x^4+2=-2x^4-x^2+x-2+2x^4+2=-x^2+x\)
\(c,H\left(x\right)=-x^2+x=x\left(1-x\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)

\(Q\left(x\right)=-3x^4+4x^3+2x^2+\dfrac{2}{3}-3x-2x^4-4x^3+8x^4+1+3x\)
\(=\left(-3x^4-2x^4+8x^4\right)+\left(4x^3-4x^3\right)+2x^2-\left(3x-3x\right)+\left(1+\dfrac{2}{3}\right)\)
\(=3x^4+2x^2+\dfrac{5}{3}\)
\(3x^4+2x^2+\dfrac{5}{3}=0\)
\(\Rightarrow3x^4+2x^2=-\dfrac{5}{3}\)(Vô lí vì \(3x^4\) và \(2x^2\) luôn lớn hơn hoặc bằng 0)
Vậy Q(x) không có nghiệm
Q(x)=3x^4+2x^2+5/3>=5/3>0 với mọi x
=>Q(x) vô nghiệm
Cho đa thức: \(f\left(x\right)=4x^3+4x^4-x^2+3x^2-3x^4-3x^3\). CMR f(x) chỉ có 1 nghiệm x=0
Giúp hộ!

\(f\left(x\right)=4x^3+4x^4-x^2+3x^2-3x^4-3x^3\)
\(\Leftrightarrow f\left(x\right)=\left(4x^3-3x^3\right)+\left(4x^4-3x^4\right)+\left(-x^2+3x^2\right)\)
\(\Leftrightarrow f\left(x\right)=x^3+x^4+2x^2\)
\(f\left(x\right)=0\)
\(\Leftrightarrow x^3+x^4+2x^2=0\)
\(\Leftrightarrow x^2\left(x+x^2+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2=0\\x+x^2+2=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x^2+\dfrac{1}{2}x+\dfrac{1}{2}x+2=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x\left(x+\dfrac{1}{2}\right)+\dfrac{1}{2}\left(x+\dfrac{1}{2}\right)+\dfrac{3}{2}=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\\left(x+\dfrac{1}{2}\right)^2+\dfrac{3}{2}>0\forall x\end{matrix}\right.\)
Vậy f(x) chỉ có 1 nghiệm

\(f\left(x\right)+h\left(x\right)-g\left(x\right)\)
\(=\left(5x^4+3x^2+x-1\right)+\left(-x^4+3x^3-2x^2-x+2\right)\)
\(-\left(2x^4-x^3+x^2+2x+1\right)\)
\(=\left(5x^4-x^4-2x^4\right)+\left(3x^3+x^3\right)+\left(3x^2-2x^2-x^2\right)\)
\(+\left(x-x-2x\right)+\left(-1+2-1\right)\)
\(=2x^4+4x^3-2x\)
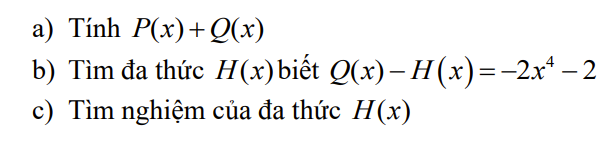
Ta có: \(F\left(x\right)+G\left(x\right)-H\left(x\right)=0\)
\(\Leftrightarrow4x^2+3x-2+3x^2-2x+5-5x^2+2x-3=0\\ \Leftrightarrow2x^2+3x=0\\ \Rightarrow x\left(2x+3\right)=0\\ \Rightarrow x=0;x=\dfrac{-3}{2}\)
Vậy tìm được x thỏa mãn là: \(x=0;x=\dfrac{-3}{2}\)