tìm M trên đường thẳng d: x+y+25=0 sao cho từ M kẻ 2 tiếp tuyến MB và MC tới (C) t/m
a/ tam giác MBC vuông
b. MNC đều
c/ Diện tích MBIC =20 ( I là tâm đường tròn )
d/ diện tích MBC =5
e/ đường thẳng BC đi qua E có (3;5)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
22 tháng 5 2022
a: Xét tứ giác MCOD có \(\widehat{MCO}+\widehat{MDO}=180^0\)
nên MCOD là tứ giác nội tiếp
b: Xét ΔMCA và ΔMBC có
\(\widehat{MCA}=\widehat{MBC}\)
\(\widehat{AMC}\) chung
Do đó; ΔMCA\(\sim\)ΔMBC
6 tháng 1 2022
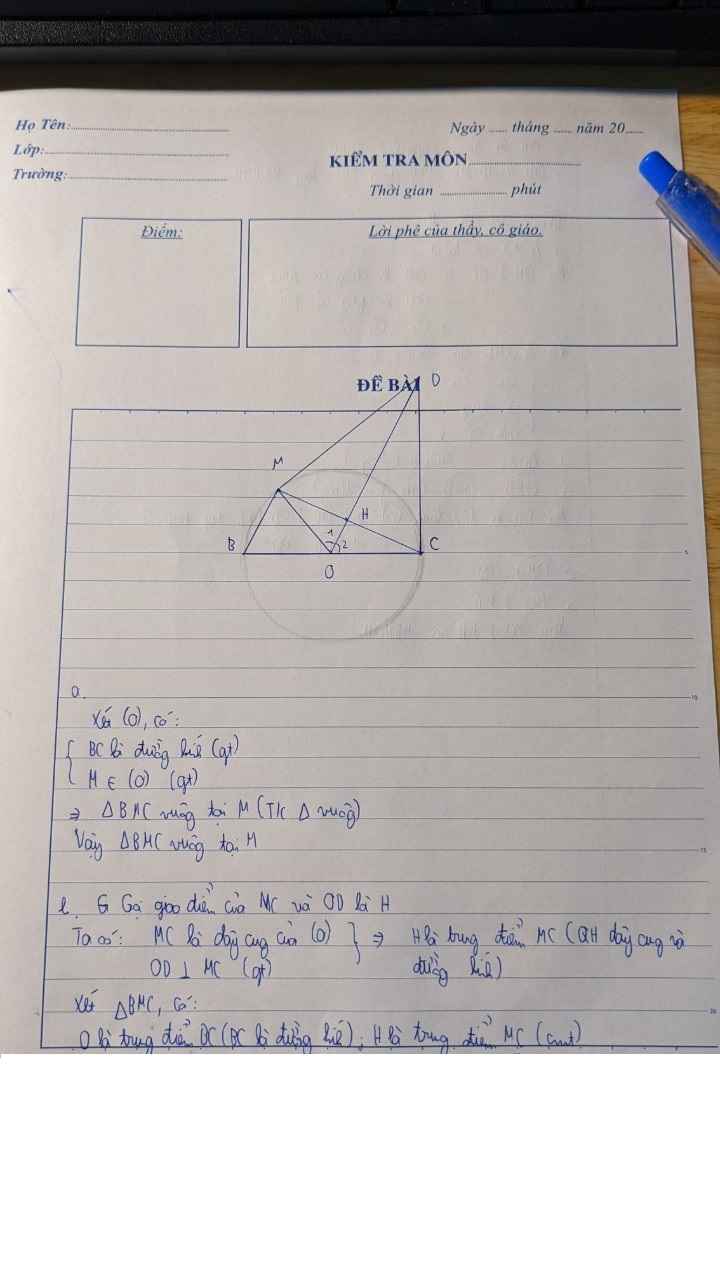
a: Xét (O) có
ΔMBC nội tiếp
BC là đường kính
Do đó: ΔMBC vuông tại M
b: MB⊥MC
OD⊥MC
Do đó: MB//OD
10 tháng 2 2023
Bài 4:
a:
Xét (O) có
ΔCED nội tiếp
CD là đường kính
=>ΔCED vuông tại E
ΔOEF cân tại O
mà OI là đường cao
nên I là trung điểm của EF
Xét tứ giác CEMF có
I là trung điểm chung của CM và EF
CM vuông góc EF
=>CEMF là hình thoi
=>CE//MF
=<MF vuông góc ED(1)
Xét (O') có
ΔMPD nội tiêp
MD là đường kính
=>ΔMPD vuông tại P
=>MP vuông góc ED(2)
Từ (1), (2) suy ra F,M,P thẳng hàng
b: góc IPO'=góc IPM+góc O'PM
=góc IEM+góc O'MP
=góc IEM+góc FMI=90 độ
=>IP là tiếp tuyến của (O')