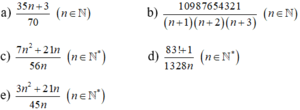Khi nào thì số thập phân vô hạn tuần hoàn dạng 0,(abc) có nghịch đảo là một số thập phân hữu hạn.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) 35 n + 3 70 = 35 n + 3 2.5.7 n ∈ ℕ vì mẫu chứa thừa số nguyên tố 7, 2 và 5 mà tử không chia hết cho 7 nên phân số viết được dưới dạng số thập phân vô hạn tuần tạp.
b) 10987654321 n + 1 n + 2 n + 3 n ∈ ℕ có mẫu là ba số tự nhiên liên tiếp nên mẫu chứa các thừa số nguyên tố 2 và 3. Mà tử không chia hết cho 3, 2 nên phân số viết được dưới dạng số thập phân vô hạn tuần tạp.
c) 7 n 2 + 21 n 56 n = 7 n n + 3 7 n .8 = n + 3 2 3 n ∈ ℕ * phân số viết được dưới dạng số thập phân hữu hạn.
d) 83 ! + 1 1328 n n ∈ ℕ *
Vì tử số là 83 ! + 1 không chia hết cho 83, mẫu 1328 n = 83.16 n ⋮ 83 n ∈ N * nên khi phân số là phân số tối giản thì mẫu vẫn chứa ước nguyên tố là 83. Lại có tử không chia hết cho 2, mẫu chia hết cho 2 nên phân số viết được dưới dạng số thập phân vô hạn tuần tạp.
e) 3 n 2 + 21 n 45 n = 3 n n + 7 3 n .15 = n + 7 3.5 n ∈ ℕ *
· Nếu lại có n chia 5 dư 3 thì phân số viết được dưới dạng số thập phân vô hạn tuần hoàn đơn.
· Nếu n chia 5 có số dư khác 3 thì phân số viết được dưới dạng số thập phân vô hạn tuần hoàn tạp.

Một phân số có mẫu dương mà mẫu có ước nguyên tố khác gì và gì thì phân số đó được viết dưới dạng số thập phân hữu hạn hả bạn

Phân số hữu hạn là : \(\frac{5}{8}=0.625,-\frac{3}{20}=-0.15\)\(\frac{14}{35}=\frac{2}{5}=0.4\) vì mẫu tối giản của chúng là tích của các lũy thừa 2 và 5.
Phân số còn lại là vô hạn tuần hoàn vì mẫu của chúng không phân tích được thành tích của các lúy thừa 2 và 5.
Số \(\frac{4}{11}=0.\left(36\right),\frac{15}{22}=0.68\left(18\right),-\frac{7}{12}=-0.58\left(3\right)\)

Ta có: \(\frac{1}{4} = 0,25\). Đây là số thập phân hữu hạn.
\( - \frac{2}{{11}} = - 0,1818....\). Đây là số thập phân vô hạn tuần hoàn. Chu kì của nó là 18. Ta viết \( - \frac{2}{{11}}=-0,(18)\)


* Rút gọn các phân số về phân số tối giản : 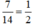
* Xét các mẫu số :
4 = 22 ; 6 = 2.3 ; 50 = 52.2 ; 125 = 53 ; 45 = 32.5 ; 2 = 21
* Các phân số viết được dưới dạng số thập phân hữu hạn là :
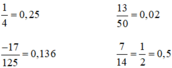
* Các phân số viết dưới dạng số thập phân vô hạn tuần hoàn là :