Câu 1:Cho góc xOy trên tia Ox lấy A , trên tia Oy lấy điểm B sao cho OA=OB . Qua trung điểm C của đoạn OA kẻ đường thẳng song song với AB cắt OB tại E . Chứng minh tứ giác ACEB là hình thang cân .
Câu 2: Cho góc xOy có số đo 700 , điểm A nằm trong góc đó . Vẽ điểmB đối xứng với A qua Ox , điểm C đối xứng với A qua Oy .
a) So sánh độ dài OB và OC .
b) Tính góc BOC
Câu 3: Cho tam giác ABC cân tại A , đường cao AH . Trên...
Đọc tiếp
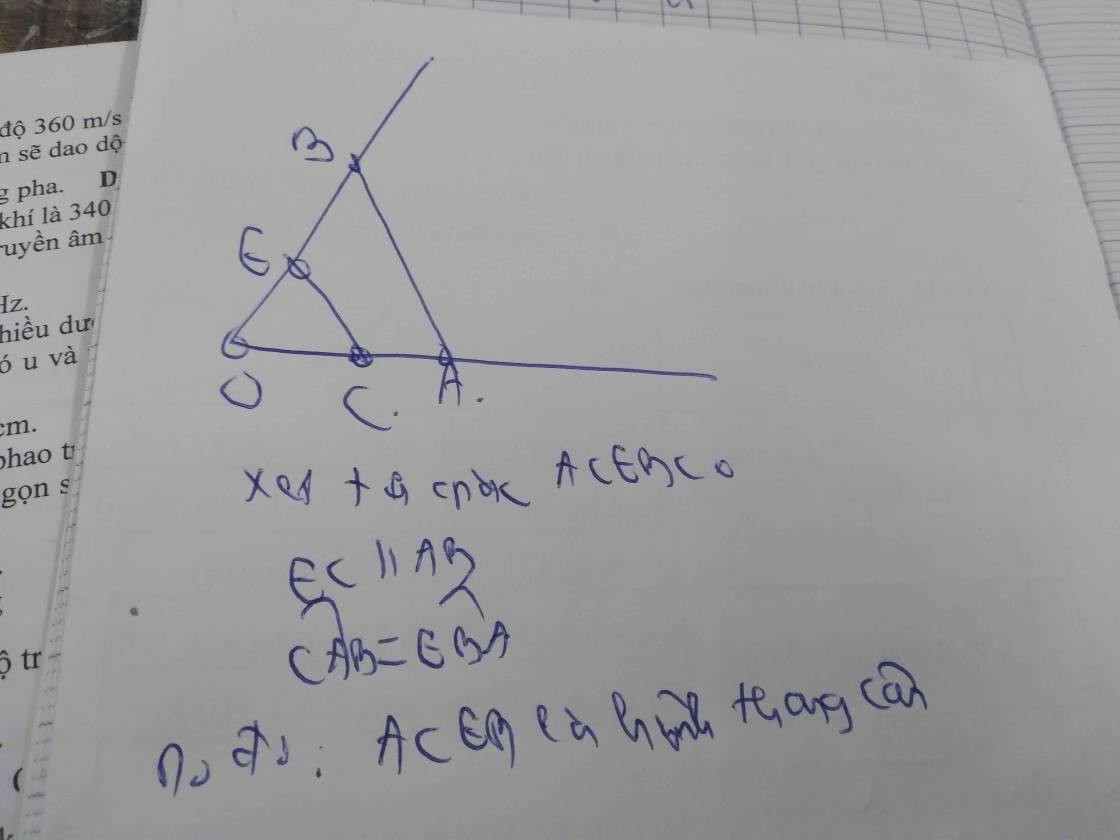
Câu 1:Cho góc xOy trên tia Ox lấy A , trên tia Oy lấy điểm B sao cho OA=OB . Qua trung điểm C của đoạn OA kẻ đường thẳng song song với AB cắt OB tại E . Chứng minh tứ giác ACEB là hình thang cân .
Câu 2: Cho góc xOy có số đo 700 , điểm A nằm trong góc đó . Vẽ điểmB đối xứng với A qua Ox , điểm C đối xứng với A qua Oy .
a) So sánh độ dài OB và OC .
b) Tính góc BOC
Câu 3: Cho tam giác ABC cân tại A , đường cao AH . Trên cạnh AB lấy điểm I , trên cạnh AC lấy điểm K sao cho AI = AK . Chứng minh rằng điểm I đối xứng với điểm K qua AH .
Câu 4: Cho tứ giác ABCD gọi E,F,G,H lần lượt là trung điểm của AB ,BC,CD,DA
a) Chứng minh rằng AM // CN
b) Kéo dài AM cắt DC tại E . Chứng minh DE = \(\dfrac{1}{2}\)EC.
Câu 2:
a: Ta có: A và B đối xứng nhau qua Ox
nên Ox là đường trung trực của AB
=>OA=OB
mà Ox là đường cao
nên Ox là tia phân giác của góc AOB(1)
Ta có: A và C đối xứng nhau qua Oy
nen OA=OC
=>ΔOAC cân tại O
mà Oy là đường cao
nên OY là phân giác của góc AOC(2)
Ta có: OA=OB
OA=OC
Do đó: OB=OC
b: Từ (1) và (2) suy ra \(\widehat{BOC}=\widehat{BOA}+\widehat{COA}=2\cdot\widehat{xOy}=140^0\)